2014-02-12
915
Если СЛУ приведена к трапецеидальному виду (например,
|
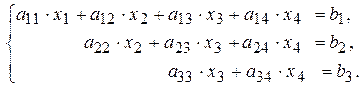
то система трапецеидального вида имеет бесконечное множество решений.
Для нахождения общего решения нужно:
1. Выбрать базисные неизвестные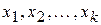 
, число которых равно числу уравнений в трапецеидальной системе. Коэффициенты при базисных неизвестных в трапецеидальной системе образуют определитель, не равный нулю. Тогда свободные неизвестные – это остальные неизвестные 
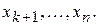(Заметим, что базисные неизвестные выбираются не единственным способом.).
2. В трапецеидальной системе перенести в правую часть уравнений слагаемые со свободными неизвестными. Тогда в левой части получится выражение треугольного вида.
3. Найти выражения базисных неизвестных через свободные неизвестные с помощью обратного хода Гаусса.
4. Записать общее решение системы. Если необходимо, из общего решения можно найти частные решения, придавая свободным неизвестным произвольные значения и вычисляя базисные неизвестные.
Пример 2. Решить систему уравнений методом исключения неизвестных.
|
|
|
|
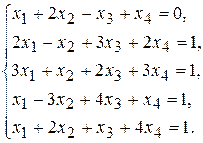
Решение
Составим расширенную матрицу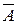 
, которая состоит из коэффициентов при неизвестных и свободных членов. Элементарные преобразования, проводимые над уравнениями, соответствуют элементарным преобразованиям над строками расширенной матрицы.
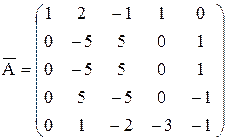
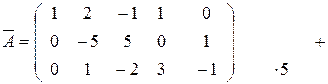
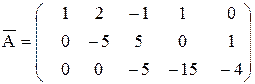
Неизвестные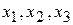 
будут базисными, т.к. определитель, составленный из коэффициентов при этих неизвестных, не равен нулю:
. Тогда 
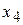- свободная неизвестная.
Перенесем слагаемые с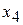 
в правую часть уравнений:
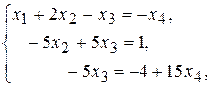
Применим обратный ход Гаусса. Выразим из последнего уравнения базисную неизвестную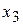 
:
.
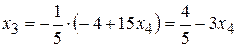Из предпоследнего уравнения найдем базисную неизвестную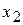 
:
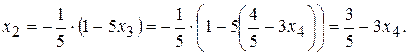
Из первого уравнения найдем базисную неизвестную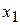 
:
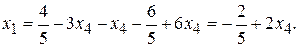
Запишем общее решение системы:
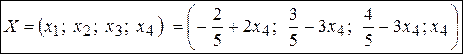, где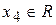 
Найдем несколько частных решений, придавая свободной неизвестной 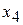произвольные значения.
Пусть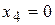 
, тогда 
, тогда частное решение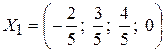 
.
Пусть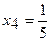 
, тогда 
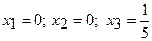, тогда частное решение 
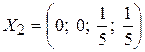, и т.д.
