Циркуляция векторного поля

Понятие циркуляции также является одним их важнейших понятий векторного анализа и его приложений. Рассмотрим какое-либо силовое поле

.

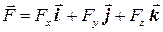Определим работу этого поля при перемещении точки вдоль некоторой кривой L от точки A до точки B. Если сила 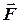однородна, а путь AB прямолинеен, то соответствующая работа будет равна скалярному произведению

.

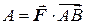Если 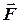– величина неоднородная, изменяющаяся от точки к точке, а L – какая-то гладкая кривая, то чтобы найти работу, нужно кривую разбить на бесконечно малые отрезки D l_i. Тогда считая, что вдоль каждого отрезка величина 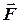однородна, то

,

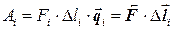где 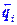– единичный вектор, совпадающий по направлению с касательной, проведенной к кривой L в какой-либо точке внутри отрезка D l_i. Чтобы найти общую работу нужно просуммировать работы по всем отрезкам:

.

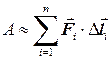Если число устремить к бесконечности, т.е. max(D l_i)®0, то вместо суммы получим интеграл

.

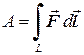Подобные интегралы в математике называют криволинейными интегралами
2-го рода.

Особое значение в векторном анализе и его приложениях имеют криволинейные интегралы, взятые по замкнутым линиям (или, как говорят, контурам). Такие интегралы называются циркуляциями и обозначаются .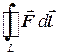

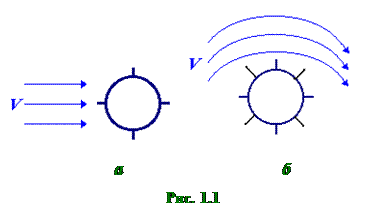
Физический смысл циркуляции рассмотрим на примере поля скоростей текущей жидкости. Предположим, что контур – окружность, например, колесо с лопастями (см. рис. 1.4). Если циркуляция равна нулю (рис. 1.4 а), то колесо вращаться не будет. Если циркуляция не равна нулю (рис. 1.4 б), то колесо будет вращаться, причем тем быстрее, чем больше величина циркуляции.