2014-02-12
1076
Понятие потока является одним из важнейших понятий векторного анализа. Оно используется при формулировании различных понятий в электродинамике, гидродинамике, термодинамике и во многих других науках.
Первоначально это понятие было введено в гидродинамике. Возьмём в поле скоростей жидкости малую плоскую площадку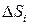 
перпендикулярную к вектору скоростей жидкости 
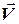(см. рис. 1.3 а). Объем жидкости, протекающей через эту площадку за время 
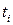, равен 
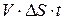. Если площадка наклонена к потоку, то соответствующий объем будет 
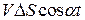, где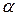 
– угол между вектором скорости 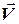и нормалью 
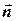к площадке 
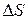(см. рис. 1.3 б). Объем жидкости, протекающей через площадку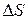в единицу времени, получится делением этого выражения на t. Он равен 
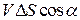, т.е. скалярному произведению 
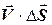вектора скорости 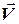на вектор площади 
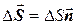. Единичный вектор 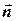нормали к площадке 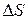можно провести в двух прямо противоположных направлениях. Одно из них условно принимается за положительное. Тогда та сторона площадки, из которой исходит нормаль, называется внешней, а та, в которую входит – внутренней.
Если поверхность S не является плоской, то ее можно разбить на достаточно малые площадки 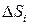, которые можно считать с достаточной степенью точности плоскими.
Тогда при вычислении объема протекающей через всю поверхность жидкости нужно просуммировать объемы жидкостей, протекающих через каждую площадку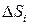
.
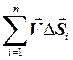Если число разбиений устремить к бесконечности, т.е.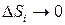 
, то вместо суммы получим интеграл
.
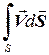Выражение подобного типа встречается в самых разнообразных разделах физики и математики и называется потоком вектора 
через поверхность 
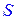, независимо от физической природы вектора 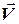. Например, в электростатике интеграл 
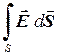называется потоком вектора напряженности электрического поля 
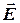, хотя с этим понятием не связано ни какое реальное течение. Введенное понятие потока векторного поля через заданную поверхность с точки зрения математики является поверхностным интегралом 2-го рода.
