2014-02-12
1139
Важной характеристикой скалярного поля U (M) является скорость изменения функции поля в указанном направлении. Если это направление совпадает с направлением одной из координатных осей, то мы получим значение соответствующей частной производной.
Из векторной алгебры известно, что координаты векторов являются по своей сути проекциями этих векторов на соответствующие координатные оси. При этом, если известны координаты какого-либо вектора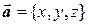 
, то можно вычислить значение проекции этого вектора на любое направление. Если это направление задано вектором 
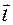, характеризующееся направляющими косинусами cosa, cosb, cosg, где a, b, g – углы, образуемые вектором 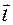с соответствующими координатными осями, то эта проекция вычисляется по формуле
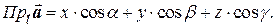(1.2)
Если считать частные производные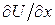 
, 
, 
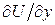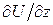аналогом векторных координат, то производная по направлению 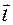будет соответствовать проекции этого вектора на ось 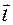и вычисляться по формуле
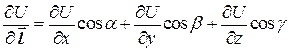. (1.3)
Пример 1.3. Дано скалярное поле U = xy + y 2+ z 2. Найти её производную в точке A (5;1;2) в направлении, идущем от этой точки к точке B (7;–1;3).
|
|
|
Решение. Найдём координаты вектора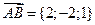 
и его длину 
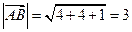. После этого находим направляющие косинусы вектора 
:
,
,
.
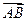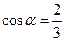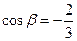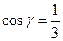Далее вычисляем частные производные:
, 
, 
,
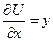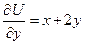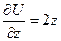и вычисляем их значения в точке A:
, 
, 
.
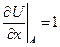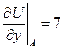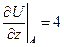Следовательно,
.
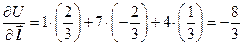Знак минус указывает, что в данном направлении скалярное поле U (x,y,z) убывает.
