Особый интерес представляет случай, когда вычисляется поток через замкнутую поверхность. Обычно в таких случаях за положительную сторону поверхности принимают ее внешнюю поверхность. Поверхностный интеграл в этом случае обозначается следующим образом:
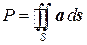 .
.
Когда векторное поле a представляет собой поле скоростей жидкости, величина потока P дает разность между количеством жидкости, вытекающей из внутренней области, ограниченной поверхностью S, и количеством, втекающей в эту область. Если P =0, то во внутреннюю область втекает столько же жидкости, сколько и вытекает. Если же P >0, то вытекает больше, чем втекает. Это означает, что внутри области имеются источники, питающие поток жидкости. В случае электрического поля, это означает, что внутри области находятся электрические заряды. Если P <0, это указывает на наличие стоков – мест, где жидкость удаляется из области.
Важнейшей характеристикой источников и стоков является дивергенция. Рассмотрим некоторую точку M векторного поля a и окружим ее замкнутой поверхностью S. Вычислим поток векторного поля через замкнутую поверхность S и возьмем отношение этого потока к объему V области, ограниченной поверхностью S:
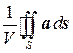 .
.
Найдем теперь предел этого отношения, при условии что область, ограниченная поверхностью S, стягивается в точку M, т.е. при V ®0. Этот предел называется дивергенцией векторного поля a в точке M:
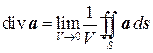 . (6.5)
. (6.5)
Ясно, что если предел существует, то он не зависит от формы поверхности S.
Дивергенция характеризует мощность источника или стока. Например, если в каждой точке поля скоростей жидкости дивергенция равна нулю, то это означает не только отсутствие источников и стоков, но и то, что жидкость не сжимается и не расширяется. Этим свойством, в частности, обладает воздух при скоростях, не превышающих примерно половины скорости звука. Однако при скоростях близких или превосходящих скорость звука, воздух ведет себя как сжимаемый газ. Тогда дивергенция такого газа будет уже отлична от нуля. Точно также дивергенция отлична от нуля, если в текущем газе возникают химические реакции (например, горение), изменяющие его плотность. В случае гравитационных или электрических полей дивергенция будет пропорциональна плотности масс или зарядов, соответственно.
Выведем теперь формулу для дивергенции в декартовой системе координат. Пусть поверхность S имеет вид прямоугольного параллелепипеда со сторонами D x, D y, D z, параллельного координатным осям (см. рис.6.6). Распишем поверхностный интеграл в определении дивергенции в виде суммы трех двойных интегралов:
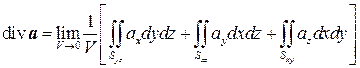 . (6.6)
. (6.6)
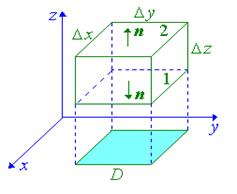 |
| Рис. 6.6 |
Рассмотрим третье слагаемое:
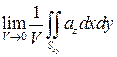
Грани 1 и 2 проецируются в одну и ту же область D на плоскости xOy (боковые грани можно не учитывать, т.к. они перпендикулярны плоскости xOy), однако их внешние нормали направлены в противоположные стороны. Считая, что уравнения граней z=z 1 и z=z 2, получим
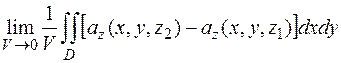 .
.
Исходя из геометрического смысла двойного интеграла (это есть объем находящийся между координатной плоскостью и поверхностью, описываемой подынтегральной функцией):
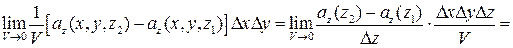
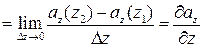 .
.
Аналогично можно получить формулы для первого и второго слагаемого в выражении
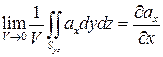 ,
, 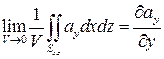 .
.
Таким образом, мы доказали следующую теорему:
Теорема. В декартовой системе координат дивергенция векторного поля a = ax i +ay j +az k вычисляется по формуле:
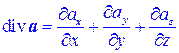 . (6.7)
. (6.7)
Например:
1) Пусть дано однородное поле: a = A i +B j +C k, где A, B, C – постоянные величины. Тогда
div a = 0.
Это означает, что если все части жидкости имеют одну и ту же скорость (т.е. жидкость движется поступательно, как твердое тело), то в таком потоке не может быть ни источников, ни стоков.
2) Пусть твердое тело вращается с постоянной угловой скоростью w. Как известно из теоретической механики линейная скорость равна v = w´ r, где r – радиус-вектор точки относительно точки вращения. Если неподвижную точку взять в качестве начала координат, а ось Oz направить вдоль оси вращения, то получим w =w k, r =x i +y j +z k. Тогда
v = –w y i + w x j. (6.8)
Это есть поле линейных скоростей вращающегося твердого тела. Вычислим дивергенцию этого поля:
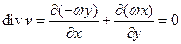 .
.
Это означает, что есть представить себе жидкость, вращающейся как твердое тело, то в таком потоке не может быть ни стоков, ни источников.
Пример 6.4. Найти дивергенцию градиента скалярного поля u = x 3 y 2 z в точке M (1;–1;1).
Решение. Найдем градиент поля
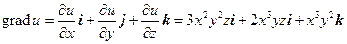 ,
,
а затем дивергенцию:
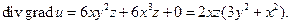
Подставляя координаты точки M, получим

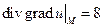 .
.
 2014-02-12
2014-02-12 5485
5485








