1) Сложение и умножение рациональных чисел являются коммутативными и ассоциативными бинарными операциями.
2) Операция вычитания на множестве рациональных чисел не коммутативна и не ассоциативна.
3) Операции объединения и пересечения подмножеств множества А коммутативны и ассоциативны на множестве Р (М).
4) Композиция функций есть ассоциативная операция. Композиция функций не коммутативна: в общем случае равенство f ◦ g = g ◦ f не выполняется.
5) На множестве Р (М) подмножеств некоторого множества, операции объединения и пересечения взаимно дистрибутивны друг относительно друга.
6) Умножение целых чисел дистрибутивно относительно сложения. Однако сложение целых чисел не дистрибутивно относительно умножения, так как в общем случае равенство a + b 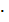 c = (a + b)
c = (a + b) 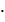 (a + c) не выполняется.
(a + c) не выполняется.
7) Сложение квадратных матриц порядка n коммутативно и ассоциативно. Умножение квадратных матриц дистрибутивно относительно сложения.
8) Умножение матриц ассоциативно, не коммутативно, умножение матриц дистрибутивно относительно сложения, то есть A 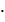 (B
(B 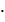 C) = A
C) = A 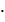 B + A
B + A 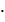 C, если произведение А
C, если произведение А 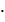 В и сумма В + С существует, и (В + С)
В и сумма В + С существует, и (В + С) 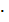 А = В
А = В 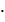 А + С
А + С 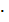 А, если произведение В
А, если произведение В 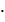 А и сумма В + С существует.
А и сумма В + С существует.
 2014-02-12
2014-02-12 871
871







