2014-02-12
3316
На практике очень часто встречаются такие испытания, число возможных исходов которых бесконечно.
Иногда в таких случаях можно воспользоваться методом вычисления вероятности, в котором по-прежнему основную роль играет понятие равновозможности некоторых событий. Применяется этот метод в задачах, сводящихся к случайному бросанию точки на конечный участок прямой, плоскости, пространства. Отсюда и возникает само название вероятности – геометрическая вероятность.
Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области.
Для определения ограничимся двумерным случаем. Одномерный и трёхмерный случаи отличаются только тем, что вместо площади в них нужно говорить о длинах и объёмах.
Пусть на плоскости имеется некоторая область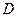 
,
площадь которой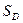 
, и в ней содержится другая
область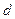 
, площадь которой 
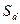. В область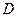
наудачу бросается точка. Спрашивается, чему равна вероятность того, что точка попадёт в область ?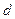
При этом предполагается, что наудачу брошенная точка может попасть в любую часть области 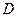, и вероятность попасть в какую-либо часть области 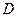пропорциональна площади этой части и не зависит от её расположения и формы. Таким образом, вероятность попадания в область 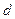при бросании наудачу точки в область :
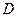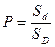
Пример: (задача о встрече) Два лица условились встретиться в определённом месте, договорившись только о том, что каждый является туда в любой момент времени между 11 и 12 часами и ждёт в течение 30 минут. Если партнёр к этому времени ещё не пришёл, или уже успел покинуть установленное место, встреча не состоится. Найти вероятность того, что встреча состоится.
Решение: Пусть х и у – моменты прихода в определённое место двух лиц.
Тогда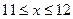 
, 
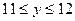
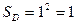
Встреча произойдёт, если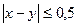 
:
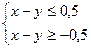
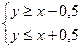
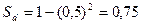
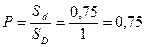
Замечание: Свойства вероятности сохраняются и при геометрическом определении вероятности.
