Определение 3.4. Если человек или группа людей оценивают вероятность наступления того или иного события на основе опыта, имеющейся информации и интуиции, то такая вероятность называется субъективной вероятностью.
Классическая и статистическая вероятности – объективные.
Субъективная вероятность включает индивидуальные суждения, информацию и другие критерии. Изучение субъективных вероятностей как области научного знания началось в 30-х гг. XX в. Поскольку идет процесс ее становления, то это – дискуссионная область теории вероятностей. Она близко ассоциируется с методами принятия решений в условиях неопределенности. Эксперт, оценивающий вероятность успеха какого-либо события, предлагает в качестве решения персональные суждения, базирующиеся на личном опыте, знании. Субъективная вероятность одного эксперта может сильно отличаться от субъективной вероятности другого при оценке одного и того же события.
Существуют различные методы оценки субъективной вероятности. Большинство из них основано на проведении опроса. Различия в методах заключаются в решении задач либо с конечным множеством событий, либо с бесконечным. Для первой задачи возможна оценка вероятности каждого события в отдельности, для второй – строятся функции распределения непрерывных случайных величин.
Примеры методов оценки субъективной вероятности:
1. Метод прямой оценки вероятности событий. В нем эксперту предоставляется список всех рассматриваемых событий (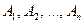 ). Эксперт для каждого рассматриваемого события должен указать вероятность или время его появления (или существования). Метод имеет различные модификации. Одна из них: предлагается сначала выбрать наиболее вероятное событие из предложенного списка, затем оценить его вероятность. Далее это событие из списка удаляется, а к оставшемуся списку применяется уже описанная процедура. Сумма всех полученных вероятностей должна равняться единице. Сам по себе метод простой, однако эксперт должен проверять условие равенства всех вероятностей единице.
). Эксперт для каждого рассматриваемого события должен указать вероятность или время его появления (или существования). Метод имеет различные модификации. Одна из них: предлагается сначала выбрать наиболее вероятное событие из предложенного списка, затем оценить его вероятность. Далее это событие из списка удаляется, а к оставшемуся списку применяется уже описанная процедура. Сумма всех полученных вероятностей должна равняться единице. Сам по себе метод простой, однако эксперт должен проверять условие равенства всех вероятностей единице.
2. Метод отношений. Эксперту вначале предлагается выбрать наиболее вероятное событие. Этому событию приписывается неизвестная вероятность 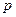 . Затем эксперт должен оценить отношение всех
. Затем эксперт должен оценить отношение всех 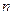 вероятностей
вероятностей 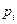 всех остальных
всех остальных 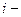 х событий к вероятности
х событий к вероятности 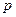 выделенного события, то есть
выделенного события, то есть 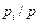 . С учетом этих отношений и соблюдая условия нормировки
. С учетом этих отношений и соблюдая условия нормировки 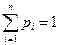 , составляется уравнение для нахождения вероятности
, составляется уравнение для нахождения вероятности 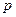 , а затем пересчитываются вероятности
, а затем пересчитываются вероятности 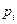 .
.
 2014-02-02
2014-02-02 3462
3462
