Распределения непрерывных случайных величин.
1. Экспоненциальный (показательный) закон распределения.
В теории массового обслуживания, в физике, биологии, вопросах надёжности и др. часто имеют дело со случайными величинами, имеющими так называемое экспоненциальное или показательное распределение.
Определение. Непрерывная с. в. Х распределена по показательному закону, если её плотность вероятности имеет вид:
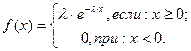
Функцию распределения для данной плотности найдём по формуле:
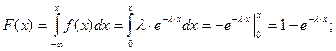
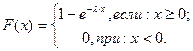
Графики функции распределения и плотности распределения для биномиального закона распределения вероятностей приведены ниже.
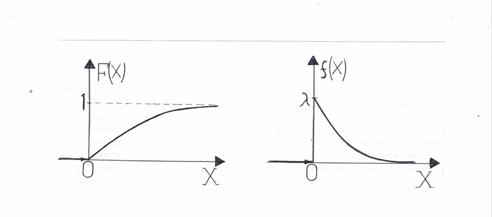
Определим числовые характеристики экспоненциального распределения.
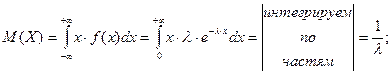
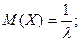
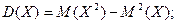
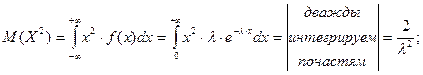
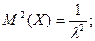
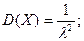

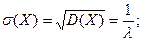
Для показательного распределения математическое ожидание и с.к.о. совпадают, что является признаком его наличия.
Пример1. Случайная величина Т – время работы до отказа мощной осветительной лампы – имеет показательное распределение. Определить вероятность того, что лампа проработает не менее 600 часов, если известно, что среднее время работы ламп такого типа равно 400 часов.
Решение.
Из условия известно, что математическое ожидание случайной величины Т равно 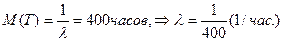 , тогда:
, тогда:
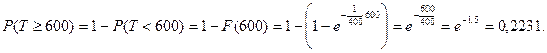
Вероятность попадания с. в. Х, распределённой по показательному закону, на заданный промежуток 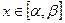 подсчитывается по формуле:
подсчитывается по формуле:
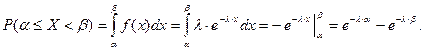
2. Нормальный (Гауссовский) закон распределения вероятности.
Нормальный закон – наиболее часто встречающийся на практике закон распределения. Его главная особенность состоит в том, что он является предельным законом, к которому стремятся распределения вероятности многих интересующих нас событий, опытов при наличии большого числа действующиъх неизвестных факторов с неизвестными законами распределения. Чем большее количество таких факторов влияет на результат интересующего нас опыта, тем ближе закон распределения вероятности к нормальному.
Такие интересующие нас случайные величины, например, как ошибки измерения расстояния до цели, промахи при стрельбе, вызывающие явление рассеивания вокруг цели и т. д. – имеют распределения, близкие к нормальному.
Определение. Закон распределения называется нормальным, если его плотность вероятности имеет вид:
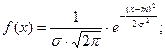
Закон распределения – двухпараметрический. Выясним смысл входящих в него параметров, для чего найдём математическое ожидание и диспнрсию.
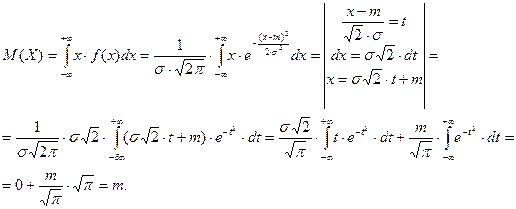
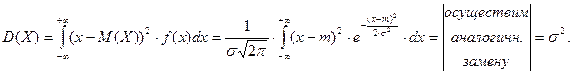
Итак, 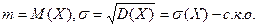
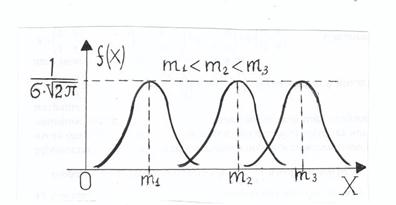 |
Влияние папраметра m на вид кривой плотности cм. ниже.
Влияние характеристики рассеивания 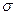 на график плотности показано на следующем рисунке.
на график плотности показано на следующем рисунке.
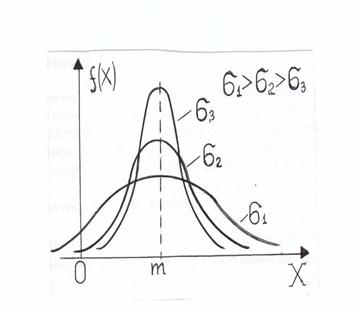
При всех трансформациях кривой плотности площадь под её графиком остаётся неизменной, равной единице:
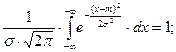
 |
Функция распределения для нормального закона.
Найдём функцию распределения по известной плотности распределения:
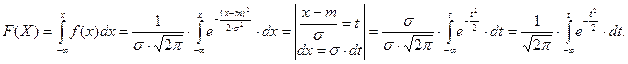
Полученный интеграл, называемый интегралом вероятности – неберущийся.
Для его вычисления используется табулированная нормированная интегральная функция, имеющая вид:
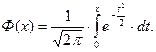
Для вычисления значения функции распределения F(х) через табулированный интеграл вероятности используют равенство:
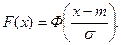
Вероятность нормально распределённой случайной величины принимать свои значения, принадлежащие интервалу 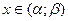 , подсчитывается по формуле:
, подсчитывается по формуле:
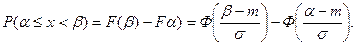
Вероятность того, что абсолютная величина отклонения возможных значений случайной величины от математического ожидания окажется меньше числа 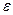
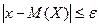 , вычисляется по формуле:
, вычисляется по формуле:
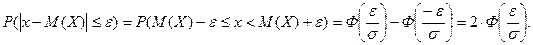
В математической статистике, после первичной обработки опытных данных, для выдвижения гипотезы о наличии закона нормального распределения часто используют правила «одного, двух и трёх сигм».
Правило «одного сигма» состоит в подсчёте вероятности попадания случайной точки в промежуток 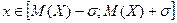 по результатам обработки опытных данных и сравнении результата с вероятностью попадания случайной точки в тот же промежуток при наличии нормального закона распределеия, которая равна:
по результатам обработки опытных данных и сравнении результата с вероятностью попадания случайной точки в тот же промежуток при наличии нормального закона распределеия, которая равна:
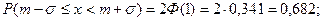
Для правила «двух сигм» контрольная цифра для нормально распределённой случайной величины равна:
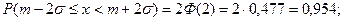
Для правила «трёх сигм» контрольная цифра равна:
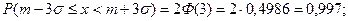
Пример 2. Самолёт совершает боевой разворот для выхода на курс судна. Далее он производит обстрел судна неуправляемыми ракетами, выпускаемыми из контейнера, неподвижно закреплённого под самолётом. Ширина судна – 8 метров, при этом полёт самолёта – вдоль оси судна, прицеливание – по оси судна. Вследствие боевого разворота самолёт имеет боковое скольжение, приводящее к систематической ошибке в попадании ракеты на 2 метра вправо по отношению к направлению пуска. Рассеивание неуправляемых ракет (это их техническая характеристика) в боковом направлении характеризуется величиной с.к.о. 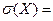 5 метров. Сколько лётчик должен пустить ракет, чтобы с вероятностью Р = 0,95 поразить судно.
5 метров. Сколько лётчик должен пустить ракет, чтобы с вероятностью Р = 0,95 поразить судно.
Решение.
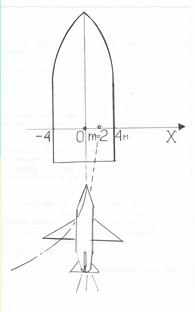
Математическое ожидание попадания с учётом бокового сноса ракет, вызванного боковым скольжением самолёта, составляет 2 метра вправо от оси судна
М(Х) = 2 м. (см. рис. ниже). Среднее квадратическое отклонение точек попадания ракет от оси судна составляет 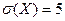 метров. Отклонение точек попадания ракет от оси судна в боковом направлении подчинено нормальному закону с параметрами m = 2 м. и с.к.о.
метров. Отклонение точек попадания ракет от оси судна в боковом направлении подчинено нормальному закону с параметрами m = 2 м. и с.к.о. 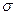 =5 м. Подсчитаем вероятность попадания при пуске одной ракеты, для чего исползуем формулу для подсчёта вероятности попадания нормально распределённой случайной величины на заданный сегмент:
=5 м. Подсчитаем вероятность попадания при пуске одной ракеты, для чего исползуем формулу для подсчёта вероятности попадания нормально распределённой случайной величины на заданный сегмент:
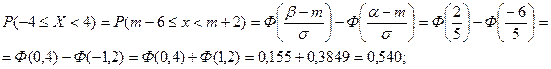
Для определения числа пущеных ракет, обеспечивающих вероятность порадения судна, равную Р = 0,95, воспользуемся теоремой о вероятности суммы совместных независимых событий.
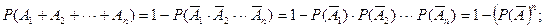
Вероятность промаха при каждом пуске равна: 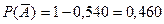 . Тогда число пущеных ракет, обеспечивающих заданную вероятность поражения судна, найдём из соотношения: 0,95=1-(0,460)n, откуда:
. Тогда число пущеных ракет, обеспечивающих заданную вероятность поражения судна, найдём из соотношения: 0,95=1-(0,460)n, откуда: 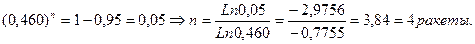
Число пущеных ракет получаем, округляя дробное число в сторону его увеличения до ближайшего целого значения.
Надёжность работы объектов.
Определение. Надёжностью называется свойство объекта выполнять заданные функции, сохраняя во времени значения установленных эксплоатационных показателей в заданных пределах.
Объекты могут находиться в двух состояниях: работоспособном и не работоспособном. Событие, заключающееся в нарушении работоспособности, наз. отказом.
Показатель надёжности объекта связан со стучайной величиной Т – времени наработки объекта до отказа. Наработка – продолжительность или объём работы объекта, измеряемые в часах, километрах, циклах или других единицах измерения.
Определение. Функцией надёжности R(t) называют функцию, выражающую вероятность безотказной работы объекта (изделия) в течение заданной наработки 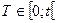 .
.
Если функция распределения случайной величины Т имеет вид F(t), то функция надёжности получает выражение:
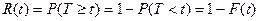 .
.
При определении показателя надёжности (значения функции R(t)) чаще всего используется показательное распределение, так как оно характерно для многих сложных систем и, кроме того, получаются относительно простые формулы для расчёта надёжности.
Пример 3. Для условия примера 1 построить график, выражающий изменение надёжности функционирования мощной осветительной лампы, в зависимости от времени её эксплоатации при использовании показательного закона для случайной величины Т.
Решение.
Функция надёжности для показательного распределения имеет вид:
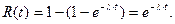
График функции приведен ниже.
При нормальном (Гауссовском) распределении случайная величина Х может принимать свои значения в бесконечном промежутке 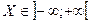 , тогда как случайная величина Т – время наработки до отказа, обычно принимает свои значения в полубесконечном промежутке
, тогда как случайная величина Т – время наработки до отказа, обычно принимает свои значения в полубесконечном промежутке 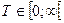 . Поэтому, в случаях, когда функция распределения F(t) имеет нормальный закон, используется усечённое нормальное распределение.
. Поэтому, в случаях, когда функция распределения F(t) имеет нормальный закон, используется усечённое нормальное распределение.
Для «усечения» какого – либо закона распределения на промежутке 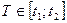 используют следующий приём:
используют следующий приём:
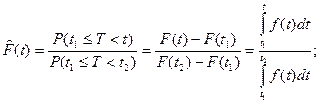
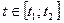
Для усечённого на 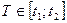 нормального распределения (случайная величина принимает свои значения только на этом промежутке) вводится нормирующий множитель:
нормального распределения (случайная величина принимает свои значения только на этом промежутке) вводится нормирующий множитель:
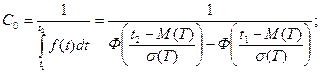
Плотность распределения усечённого на 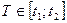 нормального закона принимает вид:
нормального закона принимает вид:
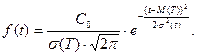
Функция распределения для усечённого на 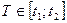 нормального закона такая:
нормального закона такая:
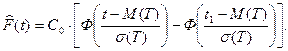
Если случайная величина Т принимает свои значения в промежутке 
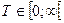 , то нормирующий множитель подсчитывается по формуле:
, то нормирующий множитель подсчитывается по формуле:
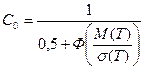 ;
;
Функция надёжности при этом получит выражение:
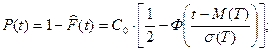
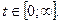
Пример 4. Тиристорный выпрямитель имеет нормальное распределение времени наработки до отказа Т с параметрами 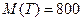 часов и с.к.о.
часов и с.к.о. 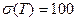 часов. Найти вероятности безотказной работы блока выпрямителя для следующих значений времени наработки:
часов. Найти вероятности безотказной работы блока выпрямителя для следующих значений времени наработки: 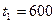 часов,
часов, 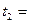 800 часов,
800 часов, 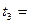 1000 часов. Построить график соответствующей функции надёжности.
1000 часов. Построить график соответствующей функции надёжности.
Решение.
Область возможных значений наработки до отказа равна 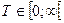 , поэтому нормирующий множитель принимает значение:
, поэтому нормирующий множитель принимает значение:
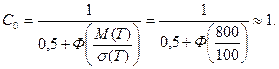
Значения функции надёжности для перечисленных в условии времён наработки, равны:
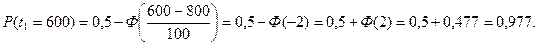
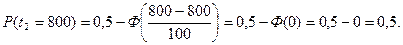
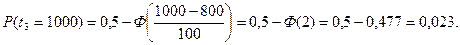
График функции надёжности приведен ниже.
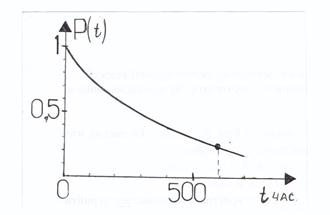
Рисунок к примеру 3.
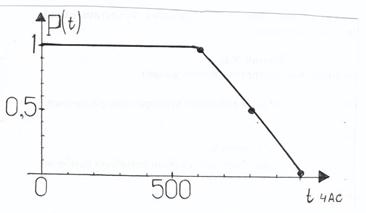
Рисунок к примеру 4.
 2014-02-09
2014-02-09 1665
1665








