Понятие о несобственном кратном интеграле по неограниченной области

Моменты инерции тела

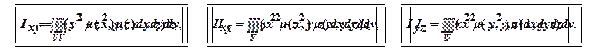
Моменты инерции тела относительно координатных плоскостей вычисляются по формулам

и моменты инерции тела относительно координатных осей

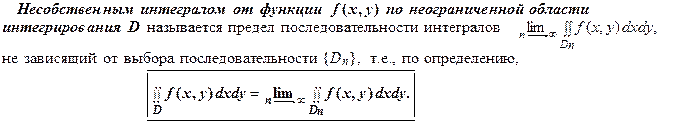
При необходимости интегрирования функций нескольких переменных по неограниченной области D поступают так. Выбирают последовательность ограниченных областей интегрирования D ₁, D ₂, D ₃,..., монотонно исчерпывающих область D, т.е. D ₁ Ì D ₂Ì D ₃Ì... и D_n ® D при n ® ¥. Например, если область интегрирования D совпадает со всей плоскостью Ох у, то за последователь { D_n } можно принять совокупность концентрических кругов x ² + y ² £ a_n ², a_n < a_{n +1}, n = 1, 2,..., где a_n ® ¥ при n ® ¥.

Если предел последовательности интегралов существует и конечен, то несобственный интеграл по неограниченной области называется сходящимся, в противном случае - расходящимся.

Пример 1. Вычислить интеграл 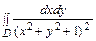, где область интегрирования D – вся плоскость.

В качестве областей интегрирования { D_n } выбираем круги х ² + у ² ≤ n ² радиуса n (n = 1, 2, …).

Переходя к полярным координатам, получим

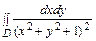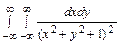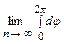
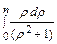= = = 2 π =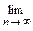

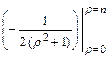= 2 π 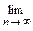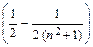= π. Интеграл сходится и равен π.

Для интеграла по неограниченной области D справедлив следующий

Признак сравнения. Если 0 ≤ f (x, y) ≤ g (x, y) 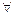(x, y) 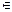D, и интеграл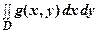

сходится, то сходится и интеграл .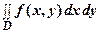

Если же интеграл 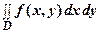расходится, то расходится и интеграл .

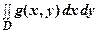Интегралы, сходящиеся на всей плоскости, можно вычислять с помощью повторного интегрирования:

= = .

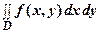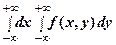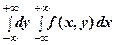Несобственные интегралы от функции трех, четырех и более числа переменных по неограниченным областям определяются аналогично.