Статические моменты тела относительно координатных плоскостей. Центр тяжести

Элементарный статический момент относительно плоскости Оху равен

dK_xy = z dm = zm (х, у, z) dv = zm (х, у, z) dxdydz,

где m (х, у, z) - плотность. Отсюда статический момент относительно плоскости Оху равен

K_xy = .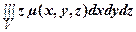

Аналогично, статические моменты относительно плоскостей Охz и Oyz равны

K_xz = 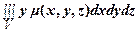и K_yz = .

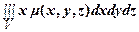Вычислив массу m тела V и его статические моменты, легко найти координаты центра тяжести тела:

x_c = 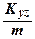= 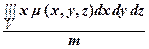, y_c = = ,

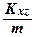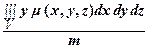z_c = = .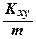

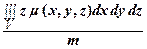Если тело однородно, то μ = const и m = μW. Отсюда (W – объем тела):

x_c = 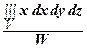, y_c = 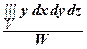, z_c = .

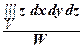Пример 6. Найти центр тяжести однородного полушария радиуса R.

Считаем, что центр тяжести шара находится в начале координат, а рассматриваемого полушария – над плоскостью Оху. В силу симметрии имеем: х_с = 0, у_с = 0. Объем шара равен W =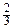π R ³. Найдем статический момент относительно плоскости Оху:

K_xy =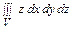==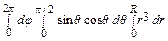 2 π =>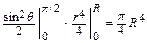

z _с = 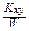= = 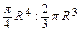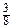R => C 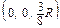– искомый центр тяжести.