Объем тела
Приложения тройного интеграла
Объем области V выражается формулой V = 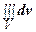 или V =
или V = 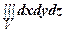 – в декартовых прямоугольных координатах;
– в декартовых прямоугольных координатах;
V = 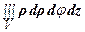 – в цилиндрических координатах;
– в цилиндрических координатах;
V = 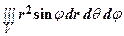 – в сферических координатах.
– в сферических координатах.
Масса тела m по заданной объемной плотности γ вычисляется по формуле
m = 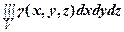 ,
,
где γ (x, y, z) – объемная плотность распределения массы в точке М (x, y, z).
Пример 6. Найти массу тела, ограниченного полусферами z =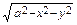 и z =
и z =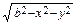 (a < b) и
(a < b) и
плоскостью Оху, если плотность в каждой точке пропорциональна расстоянию от этой точки до начала координат.
m =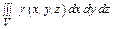 =
=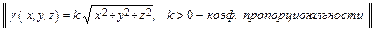 =
= 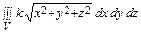 .
.
Переходя к сферическим координатам, получим V ٭ = 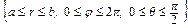 и
и
m = k 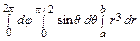 = k · 2 π ·
= k · 2 π · 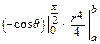 =
= 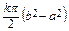 .
.
 2014-02-12
2014-02-12 1162
1162








