Простейшие задачи, вытекающие из определения ДУ 1-го порядка

Задача-1. Пусть заданы: ДУ в виде y′ = f (x,y), или F(x, y, y′), а также функция y = φ (x). Нужно определить является ли решением заданного ДУ.

Решение: Так как функция y=φ (x) должна превращать в тождество дифференциальное уравнение 1-го порядка, то подставлять в уравнение необходимо не только саму функцию, но и ее производную y′. Это определяет общую схему решения задачи:

1). Пусть имеем дифференциальное уравнение F(x,y, y′)=0 и необходимо проверить является ли данная функция y=φ (x) решением этого уравнения.

2). Вычисляем производную заданной функции y′ = φ′ (x).

3). Подставляем в уравнение функцию y=φ (x) и ее производную y′ = φ′ (x).

4). Если уравнение F(x, φ (x), φ′ (x)) = 0 обратилось в тождество, функция y = φ (x) является решением уравнения F(x,y,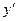)=0, иначе – не является.

5). Записываем ответ: функция y=φ (x) является (не является) решением заданного ДУ.

Ответ: Является (Не является).

Задача-2. Пусть задано семейство кривых: y = φ (x,С). Построить ДУ, для которого это семейство является решением..

Решение: при выполнении задания необходимо знать, что семейство кривых может быть задано в виде функции с параметром: y=φ (x,С). Оказывается можно построить дифференциальное уравнение F(x, y, y ′)=0, решением которого является функция y = φ(x,С).

Общая схема выполнения задания такова:

1). Пусть имеем семейство кривых y=φ (x,С).

2). Вычислим производную y ′= φ ′(x,С).

3). Имея систему: 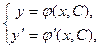исключим параметр С из первого выражения, используя второе, или наоборот (способ каждый выбирает сам!):

а) выразим из y=φ (x,С) параметр С=f₁ (x,y) и подставим его выражение для производной y ′= φ ′(x,С); полученное выражение y ′= φ ′(x,f₁ (x,y)) является искомым дифференциальным уравнением, для которого решением является заданное семейство кривых y=φ(x,С);

б) выразим из y ′= φ ′(x,С) параметр С=f₂ (x,y ′) и подставим его выражение для семейства кривых y=φ (x,С); полученное выражение y=φ (x,f₂ (x,y ′)) является искомым дифференциальным уравнением, для которого решением является заданное семейство кривых y=φ (x,С);

5). Записываем ответ: семейство кривых y=φ (x,С) определяет дифференциальное уравнение: y ′= φ ′(x,f₁ (x,y)) - из п. 3_а) (или y=φ (x,f₂ (x,y ′)) - из п. 3_б)).

Ответ: Запись найденного ДУ (записи у разных авторов могут отличаться, не принципиально!).

§ 4. ДУ 1-го порядка с разделяющимися переменными

ДУ 1-го порядка с разделяющимися переменными можно отнести к самому важному виду уравнений. Оказывается, почти все изучаемые дифференциальные уравнения на заключительном этапе используют приемы разделения переменных.

Рассмотрим два принципиально различных вида уравнений с разделяющимися переменными:

А. Форма записи уравнения: y′=f (x) ∙g (y);

В. Форма записи уравнения: f ₁(x) ∙g ₁(y) dx+f ₂(x) ∙g ₂(y) dy = 0;

С. Форма записи уравнения: y′=f (ax+by+c).

Решение–А: при выполнении задания необходимо знать, что уравнение с разделяющимися переменными необходимо привести к виду: f ₁(y) dy = f ₂(x) dx, после чего его можно интегрировать. При переходе от записи y′=f (x) ∙g (y) к записи f ₁(y) dy=f ₂(x) dx могут использоваться неэквивалентные преобразования (например, деление на алгебраическое выражение). Эти ситуации требуют дополнительных исследований с целью выявления всех возможных решений заданного уравнения.

Общая схема решения уравнения такова:

0). Запишем уравнение в форме: dy = f (x) ∙g (y) dx (для анализа и решения удобнее).

1). Если возможно равенство: g (y₀) = 0, то функция y=y₀ (прямая, параллельная оси OX) есть решение уравнения в исходной записи.

2). Учитывая, что теперь g (y)≠0), запишем уравнение в форме: 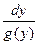= f (x) ∙dx. (1)

3). Интегрируем уравнение (1): 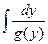=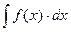+ C ₁ – общий интеграл ДУ.

4). При оформлении «Ответа» записываем общее решение заданного ДУ: F (x, y, C ₁)=0 и добавляем решение: y=y₀, если имеет место равенство: g (y₀) = 0.

Решение–В: при выполнении задания необходимо знать, что уравнение с разделяющимися переменными необходимо привести к виду: φ ₁(y) dy + φ ₂(x) dx= 0, после чего его можно интегрировать. При переходе от записи f ₁(x) ∙g ₁(y) dx+f ₂(x) ∙g ₂(y) dy =0 к записи φ ₁(y) dy + φ ₂(x) dx= 0 могут использоваться неэквивалентные преобразования (например, деление на алгебраическое выражение). Эти ситуации требуют дополнительных исследований с целью выявления всех возможных решений заданного уравнения.

Общая схема решения уравнения такова:

1). Если возможно равенство: g₁(y₀)= 0, то y=y₀ (прямая, параллельная оси OX) является решением заданного уравнения. Его необходимо учесть при записи ответа. Также, если возможно равенство: f₂(x₀)= 0, то x=x₀ (прямая, параллельная оси OY) является решением заданного уравнения. Его тоже необходимо учесть при записи ответа, т.е. общего решения ДУ.

2). Учитывая, что теперь g₁(y₀) ≠0 и f₂(x₀) ≠0, преобразуем исходное уравнение к виду: 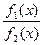dx+ 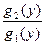dy =0. (1)

3). Интегрируем уравнение (1): 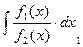+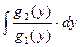= C ₁– общий интеграл ДУ.

4). Записываем ответ: F (x, y, C ₁)=0 – общее решение, также решения: y=y₀ и x=x₀ (если имеют место равенства: g₁(y₀) =0 и f₂(x₀)= 0.

Решение–С: случай интересен тем, что при решении уравнения: y′=f (ax+by+c) используется замена функции y = y (x) функцией u = u (x).

Общая схема решения уравнения такова:

0). Запишем уравнение в виде: by′=bf (ax+by+c), для удобства!

1). Примем: u = ax+by+c и продифференцируем это равенство по x: u′ = a+by′, или by′ = u′ – a.

2). Так как функция u = u (x) должна быть решением заданного уравнения, то необходимо: u′ – a = bf (u), или u′ = bf (u)+ a = φ (u). Для удобства исследований и решения: dy = φ (u) dx

3). Уравнение u′ = φ (u) решается по рассмотренной схеме Решение–А (простейший случай). После получения решения u = u (x) остается выразить y = y (x), используя выражение замены: u = ax+by+c. Замечание: цепочку преобразований перехода от заданного ДУ: u = ax+by+c → u′ = bf (u)+ a → u = u (x) → y = y (x) нужно выполнять как стандартную «технологию»!