Уравнения Бернулли
Внешне уравнение Бернулли отличается от линейного уравнения 1-го порядка только множителем y n в правой части.
| Определение: (2.1) | Дифференциальное уравнение 1-го порядка F (x, y, y′)=0 называют уравнением Бернулли, если оно линейно относительно x, y, y′ и имеет вид»: y′ + P (x)∙ y = Q (x) y n, (1) где P (x) и Q (x) – непрерывные функции от х или постоянные; n≠ 0,1. |
Замечание: Требования n ≠ 0,1 обеспечивают несовпадение с «линейным уравнением»!
Способ решения:
▪ делим (1) на y n, получаем: y –n y′ + P (x)∙ y –n+1= Q (x); (2)
▪ примем: z = y –n+1 → z′ =(– n +1) y –n∙ y′;
▪ умножим уравнение (2) на (– n +1) → (– n +1) y –n y′ +(– n +1) P (x)∙ y –n+1=(– n +1) Q (x) и учтем подстановку: z = y –n+1 → z′ +(– n +1) P (x)∙ z =(– n +1) Q (x), (3)
или z′ + P1 (x)∙ z = Q1 (x), (4)
то есть уравнение Бернулли достаточно просто преобразуется в линейное!
Замечание: При решении конкретного уравнения Бернулли необходимо максимально использовать готовый результат в виде формул (3) и (4), а не «выводить» их каждый раз заново!
Внешне уравнение в полных дифференциалах ни отличается от рассмотренных уравнений с разделяющимися переменными: М (x, y) dx+N (x, y) dy =0. По виду выражений мы устанавливали факт: относится уравнение к уравнению с разделяющимися переменными или нет. Оказывается для уравнения в полных дифференциалах тоже есть отличительный признак!
| Определение: (3.1) | Дифференциальное уравнение 1-го порядка F (x, y, y′)=0 называют уравнением в полных дифференциалах, если функции М (x, y) и N (x, y) непрерывны и дифференцируемы, а также выполняется условие:
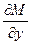 = =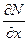 , (1)
причем частные производные , (1)
причем частные производные 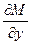 и и 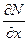 – непрерывные функции в области D. – непрерывные функции в области D.
|
Замечание: Требования содержат частные производные. Техника их вычисления принципиально не отличается от привычного дифференцирования функции одной переменной!
Затронем понятие «полный дифференциал» для функции u (x, y). Если хотят вычислить полный дифференциал функции u (x, y):
du =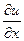 dx +
dx +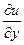 dy. (2)
dy. (2)
Если в частном случае u (x, y)=const, то du =0. Для этого случая запишем du =0 и заданное уравнение одно под другим:
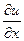 dx +
dx +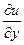 dy =0, (3)
dy =0, (3)
М dx + N dy = 0. (4)
Если выражения (3) и (4) тождественно равны, то М =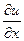 и N =
и N =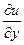 . По условию функции М (x, y) и N (x, y) непрерывны и дифференцируемы → следует непрерывность и дифференцируемость функций:
. По условию функции М (x, y) и N (x, y) непрерывны и дифференцируемы → следует непрерывность и дифференцируемость функций: 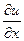 и
и 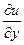 . Запишем производные:
. Запишем производные:
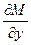 =
= 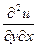 ;
; 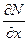 =
= 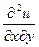 .
.
Известно, что для непрерывных и дифференцируемых функций в области D выполняется равенство:
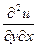 =
=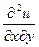 , то есть выполняется:
, то есть выполняется: 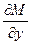 =
=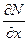 .
.
Условие (1) является необходимым условием того, чтобы левая часть уравнения (4) была полным дифференциалом некоторой функции u (x, y)=const.
Способ решения:
▪ так как М =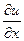 , то функцию u (x, y) можно найти как первообразную:
, то функцию u (x, y) можно найти как первообразную:
u (x, y)= 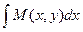 + φ(y), (5)
+ φ(y), (5)
где φ(y) отражает ту часть функции u (x, y), которая была «уничтожена» при дифференцируемости по переменной х;
▪ подберем φ(y) так, чтобы выполнялось условие: 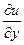 = N (x, y); это значит, что выполняется:
= N (x, y); это значит, что выполняется:
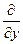
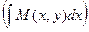 + φ′(y)= N (x, y); (6)
+ φ′(y)= N (x, y); (6)
▪ используя (6), запишем равенство для вычисления функции φ′(y):
φ′(y)= N (x, y)– 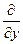
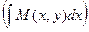 ; (7)
; (7)
▪ интегрируем (7) и окончательно «восстанавливаем» функцию u (x, y):
φ(y)=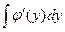 +С; (8)
+С; (8)
▪ записываем общее решение уравнения:
u (x, y)= 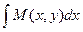 +
+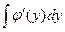 +С; (9)
+С; (9)
Замечание: При решении конкретного уравнения в полных дифференциалах необходимо максимально использовать готовый результат в виде формул (1), (7) и (9), а не «выводить» их каждый раз заново!
Вопросы для самопроверки:
1. Какое уравнение называют линейным?
2. Как записывают линейное уравнение в «стандартной» форме?
3. Какое уравнение называют уравнением Бернулли?
4. Как записывают уравнение Бернулли в «стандартной» форме?
5. Какое уравнение называют уравнением в полных дифференциалах?
6. Как записывают уравнение в полных дифференциалах в «стандартной» форме?
7. Как выполняются требования Теоремы «существования и единственности» для линейного уравнения?
8. Как выполняются требования Теоремы «существования и единственности» для уравнения Бернулли?
9. Как выполняются требования Теоремы «существования и единственности» для уравнения в полных дифференциалах?
< * * * * * >
 2014-02-12
2014-02-12 637
637







