Однородные дифференциальные уравнения. Однородные дифференциальные уравнения интересны тем, что достаточно просто приводятся к уравнениям с разделяющимися переменными

Однородные дифференциальные уравнения интересны тем, что достаточно просто приводятся к уравнениям с разделяющимися переменными, т.е. всегда интегрируются.

Определение: (1.6)

Дифференциальное уравнение называется однородным, если: А. В записи y′=f (x,y) функция f (x,y) – однородная нулевого порядка. В. В записи f ₁(x,y) dx+f ₂(x,y) dy =0 функции f ₁(x,y) и f ₂(x,y)– однородные функции одного порядка.

Начнем с однородного ДУ типа А, т.к. решение ДУ типа В осуществляется сведением его к решению первого!

Решение–А: учтем, что заданное уравнение можно записать в виде: y′= 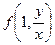. (1)

Общая схема решения уравнения y′=f (x,y) такова:

1). Выделяем возможные решения исходного уравнения: f (x,y₀)=0. Это дает одно из решений: y = y₀ – прямая, параллельная оси ОХ.

2). Примем 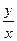= u (x). Тогда: y = ux → её производная: y′ = u′x+u.

3). Подставим в исходное уравнение (1) функцию y = ux и её производную y′ = u′x+u. Получим уравнение u′x+u = f (u) или в более удобном виде u′ = f (u)– u. (2)

4). Уравнение (2) может иметь решение при условии: φ (u₀) = f (u₀)– u₀ =0. Это даст решение в виде прямой линии: u=u₀, или y=u₀ x.

5). Далее делением на выражение f (u)– u (учтем, что теперь f (u)– u ≠ 0) получаем уравнение с разделяющимися переменными: =.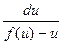

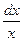6). Интегрируем уравнение (1): 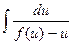= lnCx.

7). Записываем ответ, учитывая что 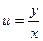. Также учитываем полученные ранее в п.1) и в п.4) решения (если они оказались возможны!).

Решение–В: учтем, что самым простым решением задачи является решение, приводящее к уже отработанной схеме решения.

Общая схема решения уравнения f ₁(x,y) dx+f ₂(x,y) dy =0 такова:

1). Выделяем возможные решения исходного уравнения. Первое: f ₁(x,y₀)=0. Это дает одно из решений: y = y₀ – прямая, параллельная оси ОХ. Второе: f ₂(x₀,y)=0. Это дает ещё одно из решений: x = x₀ – прямая, параллельная оси ОY.

2). Для уравнения: f ₁(x,y) dx+f ₂(x,y) dy = 0 запишем очевидное преобразование: y′= 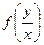, где 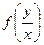=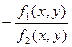, где правая часть является однородной функцией нулевого порядка, так как f ₁(x,y) и f ₂(x,y)–однородные функции одного порядка. Здесь учтено: f ₂(x,y) ≠ 0.