Симплекс-метода

Симплекс-метод. Геометрическая интерпретация

Симплекс-метод решения ЗЛП

Ранее были рассмотрены основные теоремы линейного программирования, из которых следует, что если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает, по крайней мере, с одним из допустимых базисных решений систе­мы ограничений. Там же был указан путь решения любой задачи линейного программирования: перебрать конечное число допустимых базисных решений системы ограни­чений и выбрать среди них то, на котором функция цели прини­мает оптимальное значение. Геометрически это соответствует пе­ребору всех угловых точек многогранника решений. Такой пере­бор в конце концов приведет к оптимальному решению (если оно существует), однако его практическое осуществление связано с огромными трудностями, так как для реальных задач число допус­тимых базисных решений хотя и конечно, но может быть чрезвы­чайно велико.

Число перебираемых допустимых базисных решений можно сократить, если производить перебор не беспорядочно, а с учетом изменений линейной функции, т.е. добиваясь того, чтобы каждое следующее решение было "лучше" (или, по крайней мере, "не хуже"), чем предыдущее, по значениям линейной функции (увеличение ее при отыскании максимума 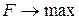, уменьшение – при отыскании минимума ).

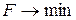Такой перебор позволяет сократить число шагов при отыска­нии оптимума. Поясним это на графическом примере.

Пусть область допустимых решений изображается многоугольником
ABCDEGH (рис. 2.1). Предположим, что его угловая точка А соответствует исходному допустимому базисному решению. При беспорядочном переборе пришлось бы испытать семь допустимых базисных решений, соответствующих семи угловым точкам многоугольника. Однако из чертежа видно, что после вершины А выгодно перейти к соседней вершине В, а затем – к оптимальной точке С. Вместо семи перебрали только три вершины, последовательно улучшая линейную функцию.

Идея последовательного улучшения решения легла в основу универсального метода решения задач линейного программирова­ния – симплексного метода (симплекс-метода).

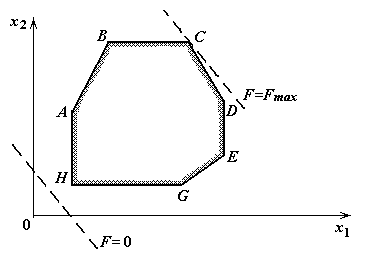
Рис. 2.1.Решение задачи линейного программирования.

Геометрический смысл симплексного метода состоит в последо­вательном переходе от одной вершины многогранника ограничений (называемой первоначальной) к соседней, в которой линейная функция принимает лучшее (по крайней мере, не худшее) значение (по отношению к цели задачи) до тех пор, пока не будет найдено оптимальное решение – вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум).

Симплексный метод, позволяющий решить любую задачу ли­нейного программирования, универсален. В настоящее время он используется для компьютерных расчетов, однако несложные при­меры с применением симплексного метода можно решать и вручную.

Для реализации симплексного метода – последовательного улучшения решения – необходимо освоить три основных элемента:

- способ определения какого-либо первоначального допустимого базисного решения задачи;

- правило перехода к лучшему (точнее, не худшему) решению;

- критерий проверки оптимальности найденного решения.

Для использования симплексного метода задача линейного программирования должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена в виде урав­нений.

Пример 2.1. Решить симплексным методом задачу:

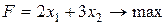
при ограничениях

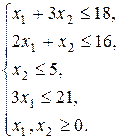(2.1)

Графическое решение задачи представлено на рис. 2.2.

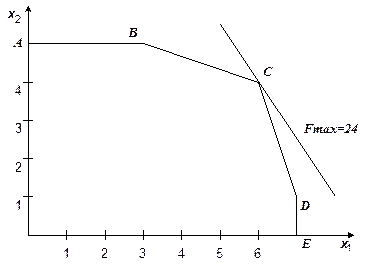
Рис. 2.2. К примеру 2.1

Решение. С помощью дополнительных неотрицательных переменных перейдем к системе уравнений. В данном случае все дополнительные переменные вводятся со знаком "плюс", так как все неравенства имеют вид "£".

Получим систему ограничений в виде

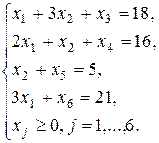(2.2)

Для нахождения первоначального базисного решения разобьем переменные на две группы – основные и неосновные. Так как определитель, составленный из коэффициентов при дополнитель­ных переменных 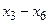, отличен от нуля, то эти переменные можно взять в качестве основных на первом шаге решения задачи. При выборе основных переменных на первом шаге не обязательно составлять определитель из их коэффициен­тов и проверять, равен ли он нулю. Достаточно воспользоваться следующим правилом:

в качестве основных переменных на первом шаге следует выбрать (если возможно) такие т переменных, каждая из которых входит только в одно из т уравнений системы ограничений, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных.

Дополнительные переменные удовлетворяют этому правилу. Если выбранные по этому правилу переменные имеют те же знаки, что и соответствующие им свободные члены в правых частях уравнений, то полученное таким образом базисное решение будет допустимым. В данном случае так и получилось.

I шаг. Основные переменные: .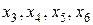

Неосновные переменные: .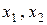

Выразим основные переменные через неосновные:

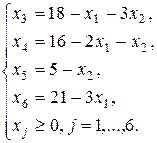(2.3)

Положив неосновные переменные равными нулю, получим базисное решение (0; 0; 18; 16; 5; 21), кото­рое является допустимым и соответствует вершине О (0;0) много­гранника OABCDE на рис. 2.2. Поскольку это решение допусти­мое, нельзя отбросить возможность того, что оно оптимально. Выразим линейную функцию через неосновные переменные:

.

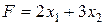В найденной точке значение функции .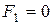

Легко понять, что функцию F можно увеличить за счет увеличе­ния любой из неосновных переменных, входящих в выражение для F c положительным коэффициентом. Это можно осуществить, перейдя к такому новому допустимому базисному решению, в котором эта переменная будет неосновной, т.е. принимать не ну­левое, а положительное значение (если новое решение будет вы­рождено, то функция цели сохранит свое значение). При таком переходе одна из основных переменных перейдет в неосновные, а геометрически произойдет переход к соседней вершине много­угольника, где значение линейной функции "лучше" (по крайней мере "не хуже"). В данном примере для увеличения F можно пе­реводить в основные либо х ₁, либо х ₂, так как обе эти переменные входят в выражение для F co знаком "плюс". Для определенности в такой х ₂ (отметим, что такое правило выбора не всегда дает наименее трудоемкое решение, иногда имеет смысл провести предварительные специальные оценки).

Система (2.3) накладывает ограничения на рост переменной х ₂. Поскольку необходимо сохранять допустимость решений, т.е. все переменные должны оставаться неотрицательными, то должны выполняться следующие неравенства (при этом х ₁ = 0 как неосновная переменная):

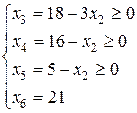, откуда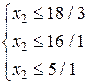

Каждое уравнение системы (2.3), кроме последнего, определяет оценочное отношение – границу роста переменной х ₂, сохра­няющую неотрицательность соответствующей переменной. Эта граница определяется абсолютной величиной отношения свободного члена к коэффициенту при х ₂ при условии, что эти числа имеют разные знаки. Последнее уравнение системы не ограничи­вает рост переменной х ₂, так как данная переменная в него не входит (или формально входит с нулевым коэффициентом). В этом случае условимся обозначать границу символом ¥. Такой же символ будем использовать, когда свободный член и коэффици­ент при переменной в уравнении имеют одинаковые знаки, так как и в этом случае нет ограничений на рост переменной.

Не накладывает ограничений на рост переменной, переводи­мой в основные, и такое уравнение, где свободный член отсутст­вует (т.е. равен 0), а переводимая переменная имеет положитель­ный коэффициент. И в этом случае граница обозначается симво­лом ¥. Обратите внимание, что при нулевом свободном члене и отрицательном коэффициенте при переводимой переменной уравнение ограничивает рост этой переменной нулем (любое положительное ее значение вносит отрицательную компоненту в следующее базисное решение).

Очевидно, что сохранение неотрицательности всех переменных (допустимость решения) возможно, если не нарушается ни одна из полученных во всех уравнениях границ. В данном примере наибольшее возможное значение для переменной х ₂ определяется как минимальное из полученных значений, т.е. х ₂ = 5. При х ₂ = 5 переменная х ₅ обращается в нуль и переходит в неосновные.

Уравнение, где достигается наибольшее возможное значение переменной, переводимой в основные (т.е. где оценка минималь­на), называется разрешающим (опорным). В данном случае – это третье уравнение.

II шаг. Основные переменные: .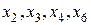

Неосновные переменные: .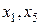

Выразим новые основные переменные через новые неоснов­ные, начиная с разрешающего уравнения:

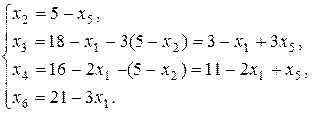(2.4)

Второе базисное решение – (0; 5; 3; 11; 0; 21) является до­пустимым и соответствует вершине А (0;5) на рис. 2.2. Геометри­ческая интерпретация перехода к новому базисному решению– переход от вершины О к соседней вершине А на многоугольнике решений OABCDE.

Выразив линейную функцию через неосновные переменные на этом шаге, получаем:

.

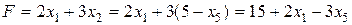Значение линейной функции 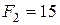. Изменение зна­чения линейной функции легко определить заранее как произве­дение наибольшего возможного значения переменной, переводи­мой в основные, на ее коэффициент в выражении для линейной функции; в данном случае .

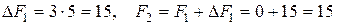Однако полученное значение F не является максимальным, так как, повто­ряя рассуждения I шага, обнаруживаем возможность дальнейшего увеличения линейной функции за счет переменной 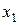, входящей в выражение для F с положительным коэффициентом. Система уравнений (2.4) определяет наибольшее возможное значение для 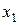: 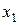= 3. Второе уравнение является разре­шающим, переменная 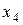переходит в неосновные, при этом .

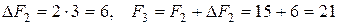III шаг. Основные переменные: .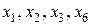

Неосновные переменные: .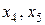

Как и на II шаге, выражаем новые основные переменные через новые неосновные, начиная с разрешающего уравнения. После преобразований получаем:

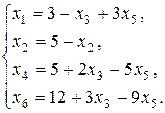(2.5)

Базисное решение (3; 5; 0; 5; 0; 12) соответствует вер­шине В (3;5). Выражаем линейную функцию через неосновные переменные: 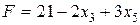. Проверяем: 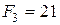. Третье допустимое базисное решение тоже не является оптимальным, поскольку при неосновной переменной х ₅ в вы­ражении линейной функции через неосновные переменные со­держится положительный коэффициент. Переводим х ₅ в основ­ную переменную. При определении наибольшего возможного значения для х ₅ следует обратить внимание на первое уравнение в системе (2.5), которое не дает ограничений на рост х ₅, так как свободный член и коэффициент при х ₅ имеют одинаковые зна­ки. Из третьего ограничения находим максимально допустимое значение х ₅ = 1. Третье уравнение является разрешающим, и переменная х ₄ переходит в неосновные;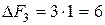

IV шаг. Основные переменные: .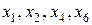

Неосновные переменные: .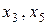

После преобразований получим:

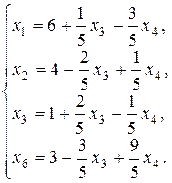
Базисное решение (6; 4; 0; 0; 1; 3) соответствует вершине С (6; 4) на рис. 2.2.

Линейная функция, выраженная через неосновные перемен­ные, имеет вид 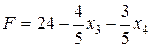. Это выражение не содержит положительных коэффициентов при неосновных переменных, поэтому функцию F не­возможно еще увеличить, переходя к другому допустимому базис­ному решению, т.е. найденное решение – оптимальное. Значение 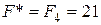– максимальное.

Теперь можно в общем виде сформулировать критерии опти­мальности решения при отыскании максимума линейной функции:

если в выражении линейной функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных пере­менных, то решение оптимально.

При определении минимума линейной функции Z возможны два пути:

1) отыскать максимум функции F, полагая F = – Z и учитывая, что ;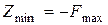

2) модифицировать симплексный метод: на каждом шаге уменьшать линейную функцию за счет той неосновной переменной, которая входит в выражение линейной функции с отрицательным коэффициентом.

Проводя рассуждения аналогично рассмотренному выше случаю, можно сформулировать критерий оптимальности при отыскании минимума линейной функции:

если в выражении линейной функции через неосновные переменные отсутствуют отрицательные коэффициенты при неосновных переменных, то решение оптимально.

2.2. Определение первоначального допустимого базисного решения

В рассмотренных выше примерах оптимальное решение по­лучено путем последовательного перехода от первоначального допустимого базисного решения к следующему, "лучшему", и так – до достижения критерия оптимальности. Однако не всегда на первом же шаге получается допустимое базисное ре­шение. В следующем примере рассмотрим один из возможных алгоритмов получения допустимого базисного решения. Дру­гой, так называемый метод искусственного базиса, будет изложен далее.

Пример 2.2. Решить симплексным методом задачу

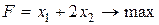
при ограничениях:

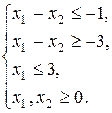
Решение. Вводим дополнительные неотрицательные пе­ременные 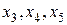с соответствующими знаками:

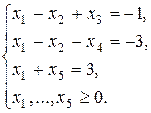
В соответствии с правилом, сформулированным в п. 2.1, на I шаге в качестве основных возьмем дополнительные переменные.

I шаг. Основные переменные: .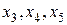

Неосновные переменные: .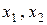

Выражаем основные переменные через неосновные:

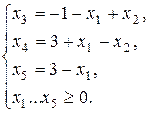
Х ₁ = (0; 0; -1; 3; 3) – первое базисное решение недопустимое (отрицательная компонента выделена), поэтому оно не может быть оптимальным. Линейная функция на недопустимом решении не рассматривается! Выберем в системе то уравнение, которое со­держит отрицательный свободный член, т.е. первое уравнение (если таких уравнений несколько, выбираем любое из них).

Поскольку переменная х ₃ принимает в первом базисном решении отрицательное значе­ние, то ее необходимо увели­чить. Это можно сделать за счет увеличения любой из неос­новных переменных, входящих в первое уравнение с положи­тельным коэффициентом, в данном случае – переменной х _2. Если перевести эту переменную в основные, то она, став по­ложительной, увеличит переменную х ₃. Как только х ₂ достиг­нет уровня 1, то х ₃ обратится в 0, т.е. исчезнет отрицательная компонента в решении. Можно считать, что переменная х ₃ станет неосновной. Однако рост переменной х ₂ ограничен условиями неотрицательности остальных переменных, которые определяют х ₂ = min{l; 3; ¥} = 1, т.е. первое уравнение – раз­решающее. При х ₂ = 1 переменная х ₃ = 0 и переходит в неосновные переменные.

II шаг. Основные переменные: .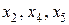

Неосновные переменные: .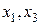

Выражая новые основные переменные через новые неосновные, начиная с разрешающего уравнения, получаем:

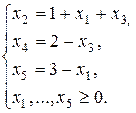
и базисное решение Х ₂ = (0; 1; 0; 2; 3), которое является допусти­мым. Поэтому выражаем через неосновные переменные целевую функцию и продолжаем решение в соответствии с алгоритмом, изложенным в п.2.1.

Замечание 1. Не всегда первый же шаг избавляет от недопустимого решения. Иногда для получения допустимого решения приходится делать несколько шагов.

Замечание 2. Если базисное решение недопустимое и для его улучшения есть возможность выбора переменной, переводимой из неосновных в основные, то рекомендуется выбрать такую неосновную переменную, которая определит в качестве разре­шающего то уравнение системы, где содержится отрицатель­ный свободный член. Только в этом случае новое базисное решение будет содержать, по крайней мере, на одну отрица­тельную компоненту меньше. Если в качестве разрешающего будет получено уравнение, не содержащее отрицательного сво­бодного члена, то в новом базисном решении число отрица­тельных компонент не уменьшится.

Сформулируем алгоритм получения первоначального допустимого решения:

1. Если каждая дополнительная переменная входит в уравнение с тем же знаком, что и свободный член, стоящий в правой части уравнения, то дополнительные пе­ременные можно брать в качестве основных на I шаге. При этом получится допустимое базисное решение.

2. Если первое базисное решение получилось недопустимым (например, в качестве основных взяты дополнительные перемен­ные, но хотя бы одна из них входила в уравнение со знаком, про­тивоположным знаку свободного члена), то рассматриваем урав­нение, содержащее отрицательный свободный член (любое, если их несколько), и переводим в основные ту неосновную перемен­ную, которая в это уравнение входит с положительным коэффи­циентом (любую, если их несколько). Такие шаги повторяем до тех пор, пока не достигается допустимое базисное решение.

3. Если базисное решение недопустимое, а в уравнении, со­держащем отрицательный свободный член, отсутствует неоснов­ная переменная с положительным коэффициентом, то в этом случае допустимое базисное решение получить невозможно, т.е. условия задачи противоречивы.

2.3. Особые случаи симплексного метода

Рассмотрим особые случаи, которые могут возникнуть при решении задачи линейного программирования симплексным методом.