Рис. 1.3. Различные случаи графического решения ЗЛП
Рис.1.2. Графическое решение ЗЛП
Возникает вопрос: как установить направление возрастания (убывания) целевой функции? Найдем частные производные целевой функции по х 1 и x 2:
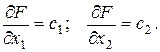
Частная производная функции показывает скорость ее возрастания вдоль данной оси. Следовательно, 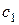 и
и 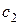 – скорости возрастания F соответственно вдоль осей Ох 1 и Ох 2. Вектор с = (
– скорости возрастания F соответственно вдоль осей Ох 1 и Ох 2. Вектор с = (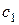 ;
;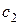 ) называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции. Вектор - с указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом.
) называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции. Вектор - с указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом.
Вектор с = (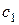 ;
;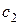 ) перпендикулярен к прямым F = const семейства
) перпендикулярен к прямым F = const семейства 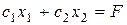 .
.
Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок ее графического решения.
1. С учетом системы ограничений строим область допустимых решений W.
2. Строим вектор с = (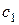 ;
;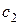 ) наискорейшего возрастания целевой функции – вектор градиентного направления.
) наискорейшего возрастания целевой функции – вектор градиентного направления.
3. Проводим произвольную линию уровня F = F 0 (проще всего провести линию F =0, перпендикулярную к вектору с).
4. При решении задачи на максимум перемещаем линию уровня F = F 0 в направлении вектора с так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точке) (на рис. 1.2 – до точки А 4). В случае решения задачи на минимум линию уровня F = F 0 перемещают в антиградиентном направлении (на рис. 1.2 – до точки А 1).
5. Определяем оптимальный план х* и экстремальное значение целевой функции F *= f (x*).
Как видно из рис. 1.3, возможны следующие случаи:
1) оптимальный план единственный: линия уровня и область допустимых решений в разрешающем положении имеют одну общую точку (рис. 1.3, а);
2) оптимальных планов бесконечное множество: в разрешающем положении линия уровня проходит через сторону области допустимых решений (рис. 1.3, б);
3) целевая функция не ограничена: линия уровня, сколько бы ее ни перемещали, не может занять разрешающего положения (рис. 1.3, в, г);
4) область допустимых решений состоит из единственной точки, где целевая функция достигает одновременно и максимального, и минимального значений (рис. 1.3, д);
5) задача не имеет решения; область допустимых решений – пустое множество, т. е. система ограничений задачи несовместна (рис. 1.3,е).
а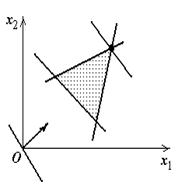 | б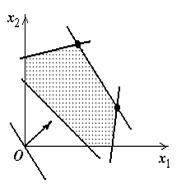 | в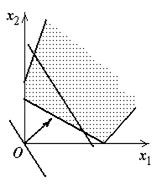 |
г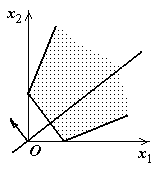 | д 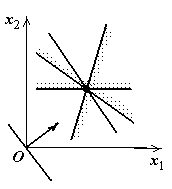 | е 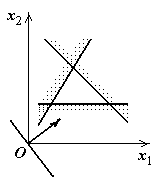 |
Пример 1.1. Цех выпускает два вида продукции, используя два вида полуфабрикатов. Продукция используется при комплектовании изделий, при этом на каждую единицу продукции первого вида требуется не более двух единиц продукции второго вида. Нормы расхода полуфабрикатов каждого вида на единицу выпускаемой продукции, общие объемы полуфабрикатов и прибыль от единицы каждой продукции представлены в табл. 1.1. Определить план производства, доставляющий максимум прибыли.
Таблица 1.1
| Полуфабрикаты | Нормы затрат на единицу продукции | Объем полуфабриката | |
| П1 | П2 | ||
| I | |||
| II | |||
| Прибыль |
Решение. Пусть 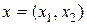 – план задачи. Тогда модель задачи:
– план задачи. Тогда модель задачи: 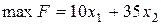 при ограничениях на полуфабрикаты
при ограничениях на полуфабрикаты 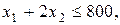
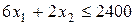 , условии комплектности
, условии комплектности 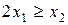 и неотрицательности переменных
и неотрицательности переменных 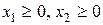 .
.
Построив соответствующие данным ограничениям-неравенствам граничные прямые 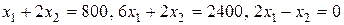 определим полуплоскости, в которых выполняются эти неравенства (рис. 1.4). Для этого достаточно взять произвольную точку, не лежащую на граничной прямой, и подставить ее координаты в неравенство. Для первых двух неравенств возьмем, например, начало координат О(0; 0). Получим истинные утверждения (0£800, 0£2400). Следовательно, первые два неравенства выполняются в полуплоскостях, содержащих точку О. Граничная прямая, соответствующая третьему неравенству, проходит через начало координат. Значит, нужно взять, например, точку (0; 10). Получаем ложное утверждение (0³10). Следовательно, третьему неравенству удовлетворяют точки полуплоскости, не содержащей пробной точки (0; 10).
определим полуплоскости, в которых выполняются эти неравенства (рис. 1.4). Для этого достаточно взять произвольную точку, не лежащую на граничной прямой, и подставить ее координаты в неравенство. Для первых двух неравенств возьмем, например, начало координат О(0; 0). Получим истинные утверждения (0£800, 0£2400). Следовательно, первые два неравенства выполняются в полуплоскостях, содержащих точку О. Граничная прямая, соответствующая третьему неравенству, проходит через начало координат. Значит, нужно взять, например, точку (0; 10). Получаем ложное утверждение (0³10). Следовательно, третьему неравенству удовлетворяют точки полуплоскости, не содержащей пробной точки (0; 10).
Поскольку 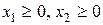 , областью допустимых решений является четырехугольник ОАВС. Далее надо построить вектор с = (
, областью допустимых решений является четырехугольник ОАВС. Далее надо построить вектор с = (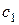 ;
;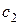 ). Так как он необходим лишь для выяснения направления возрастания целевой функции, иногда для большей наглядности удобно строить вектор l с (l>0). В нашем примере взято l=10 и построен вектор l с =(100; 350). Перпендикулярно к этому вектору проводим линию уровня F= 0. Параллельным перемещением прямой F =0 находим точку А, в которой целевая функция достигает максимума.
). Так как он необходим лишь для выяснения направления возрастания целевой функции, иногда для большей наглядности удобно строить вектор l с (l>0). В нашем примере взято l=10 и построен вектор l с =(100; 350). Перпендикулярно к этому вектору проводим линию уровня F= 0. Параллельным перемещением прямой F =0 находим точку А, в которой целевая функция достигает максимума.
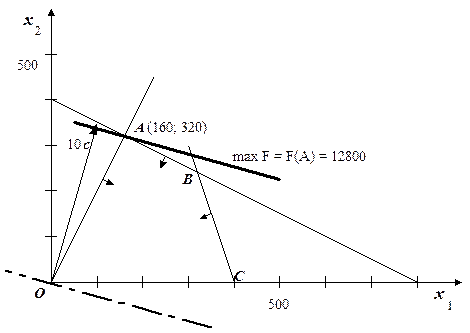
Рис. 1.4. К примеру 1.1.
Решая совместно уравнения граничных прямых АВ и ОА, находим координаты точки А: х 1=160, х 2=320. При этом F *=12800.
Итак, по оптимальному плану следует выпускать 160 ед. продукции П1 и 320 ед. продукции П2, что принесет прибыль в 12800 р.
В рассмотренных задачах максимум и минимум линейной функции достигался в одной точке, так что задачи имели единственное оптимальное решение. На практике нередко встречаются задачи, которые этим условиям не удовлетворяют. В подобных случаях геометрический метод также позволяет получить ответ.
Пример 1.2. Решить геометрически следующие задачи:
а) 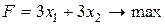 при ограничениях: при ограничениях: 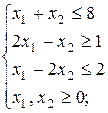 | б) 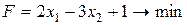 при ограничениях: при ограничениях: 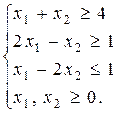 |
а) Геометрическое решение задачи показано на рис. 1.5,а, из которого следует, что линия уровня с максимальным уровнем совпадает с граничной линией АВ многоугольника решений ABCD, т.е. с линией 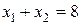 . Следовательно, на всем отрезке АВ линейная функция
. Следовательно, на всем отрезке АВ линейная функция 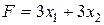 принимает одно и то же максимальное значение, равное
принимает одно и то же максимальное значение, равное 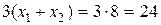 . Это означает, что задача имеет бесконечно много оптимальных решений (их задают координаты точек отрезка АВ), среди которых базисных оптимальных решений два – соответственно в угловых точках А (3; 5) и В (6; 2). Точки отрезка АВ задаются уравнением
. Это означает, что задача имеет бесконечно много оптимальных решений (их задают координаты точек отрезка АВ), среди которых базисных оптимальных решений два – соответственно в угловых точках А (3; 5) и В (6; 2). Точки отрезка АВ задаются уравнением 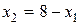 , где
, где 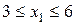 .
.
Итак, 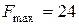 при бесконечном множестве оптимальных решений
при бесконечном множестве оптимальных решений 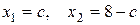 , где
, где 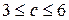 .
.
Замечание. При геометрическом решении подобных задач важно точно установить, действительно ли совпадает линия уровня с границей многоугольника решений или это связано с неточностью построений, мелким масштабом рисунка и т.п. Ответ на этот вопрос будет положительным, если линия уровня и граничная прямая параллельны, т.е. их коэффициенты при переменных пропорциональны. В рассматриваемом примере коэффициенты при переменных линии уровня 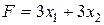 пропорциональны соответствующим коэффициентам граничной прямой
пропорциональны соответствующим коэффициентам граничной прямой 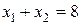 .
.
 а а | 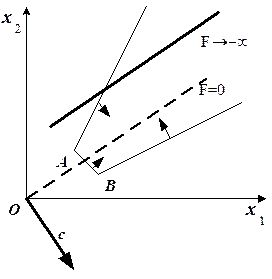 б б |
Рис. 1.5. К примеру 1.2.
б) Геометрическое решение задачи показано на рис. 1.5, б, из которого следует, что если линию уровня перемещать в направлении убывания линейной функции (т.е. в направлении, противоположном вектору c), то она всегда будет пересекать многоугольник решений, следовательно, линейная функция неограниченно убывает.
Итак, конечного оптимума линейной функции нет, т.е. 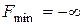 .
.
Перейдем к геометрической интерпретации ЗЛП с п переменными:
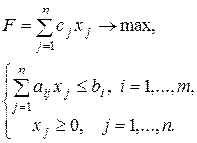 (1.2)
(1.2)
Каждое ограничение-неравенство системы (1.2)задает полупространство п -мерного пространства, являющееся выпуклым множеством. Множество планов, удовлетворяющих системе ограничений ЗЛП (1.2), представляет собой пересечение конечного числа полупространств и потому является выпуклым. Отсюда следует, что множество планов ЗЛП выпукло.
Множество планов ЗЛП в практически важных случаях чаще всего представляет собой либо выпуклый многогранник, либо выпуклую многогранную область.
Целевую функцию геометрически можно рассматривать как семейство параллельных гиперплоскостей 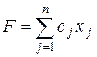 , каждой из которых соответствует определенное значение параметра F. Вектор с = (
, каждой из которых соответствует определенное значение параметра F. Вектор с = (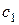 ; …;
; …; 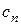 ), перпендикулярный к гиперплоскостям F =const, указывает направление наискорейшего возрастания функции F.
), перпендикулярный к гиперплоскостям F =const, указывает направление наискорейшего возрастания функции F.
С учетом сказанного, задача (1.2) геометрически сводится к нахождению точки х* многогранника (многоугольной области), определяемого неравенствами-ограничениями, через которую проходит гиперплоскость, соответствующая наибольшему значению F.
Графическим методом можно решить ЗЛП с п >2 переменными, если в ее канонической записи число неизвестных п и число линейно независимых уравнений т связаны соотношением 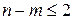 . В этом случае, выделив свободные переменные и выразив через них базисные переменные, каноническую форму задачи преобразовывают в задачу, которая будет содержать не более двух переменных. Решая эту задачу графически, находят два компонента оптимального плана. Подставляя их в ограничения задачи, определяют и остальные компоненты.
. В этом случае, выделив свободные переменные и выразив через них базисные переменные, каноническую форму задачи преобразовывают в задачу, которая будет содержать не более двух переменных. Решая эту задачу графически, находят два компонента оптимального плана. Подставляя их в ограничения задачи, определяют и остальные компоненты.
Пример 1.3. Двум погрузчикам разной мощности за 24 часа нужно погрузить на первой площадке 230 т, на второй – 168 т. Первый погрузчик на первой площадке может погрузить 10 т в час, на второй – 12 т. Второй погрузчик на каждой площадке может погрузить по 13 т в час. Стоимость работ, связанных с погрузкой 1 т, первым погрузчиком на первой площадке 8 р., на второй – 7 р., вторым погрузчиком на первой площадке 12 р., на второй – 13 р. Нужно составить план работы, т. е. найти, какой объем работ должен выполнить каждый погрузчик на каждой площадке, чтобы стоимость всех работ по погрузке была минимальной. Причем по техническим причинам первый погрузчик на второй площадке должен работать не более 16 часов.
Решение. Обозначим через 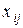 объем работ (в тоннах) i -го погрузчика на j- й площадке. Построим математическую модель задачи. Целевая функция описывает затраты, связанные с выполнением всех работ:
объем работ (в тоннах) i -го погрузчика на j- й площадке. Построим математическую модель задачи. Целевая функция описывает затраты, связанные с выполнением всех работ:
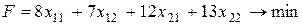 .
.
Ограничения на лимиты рабочего времени:
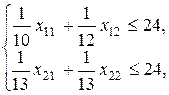
на необходимость выполнить задание:
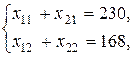
условие неотрицательности
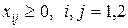 .
.
Исключим из модели переменные 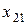 и
и 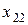 . Из ограничений-равенств имеем:
. Из ограничений-равенств имеем:
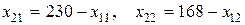 .
.
Подставив выражения для 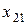 и
и 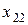 в ограничения-неравенства и целевую функцию и учитывая неотрицательность всех переменных, получим ЗЛП с двумя переменными
в ограничения-неравенства и целевую функцию и учитывая неотрицательность всех переменных, получим ЗЛП с двумя переменными  и
и 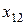 .
.
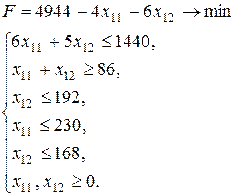
Очевидно, что целевая функция 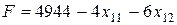 достигает минимального значения при условии, что
достигает минимального значения при условии, что 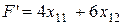 принимает максимальное значение. Имеем задачу:
принимает максимальное значение. Имеем задачу:
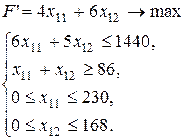
Ее графическое решение представлено на рис. 1.5.
Функция F' достигает наибольшего значения при  =100 и
=100 и 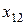 =168.Из выражений для
=168.Из выражений для 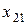 и
и 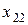 получим:
получим: 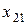 =130 и
=130 и 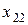 =0. Итак, по оптимальному плану первый погрузчик должен погрузить 100 т на первой площадке и 168 т на второй, второму погрузчику надлежит погрузить 130 т на первой площадке. Стоимость всех работ составит 3536 р. (F * = 4944 – 4*100 – 6*168 = 3536).
=0. Итак, по оптимальному плану первый погрузчик должен погрузить 100 т на первой площадке и 168 т на второй, второму погрузчику надлежит погрузить 130 т на первой площадке. Стоимость всех работ составит 3536 р. (F * = 4944 – 4*100 – 6*168 = 3536).
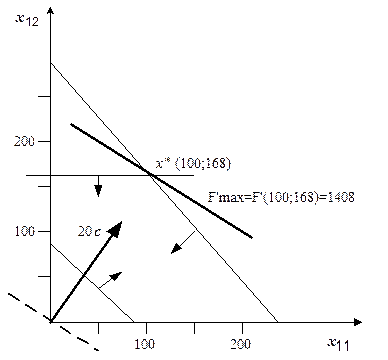
Рис. 1.5. К примеру1.3.
Анализируя рис. 1.2-1.5, легко заметить, что в ЗЛП с двумя переменными экстремум достигается в вершине области допустимых решений. Оказывается, это не случайный факт. Дальше будет доказано, что и в
п -мерном пространстве экстремум целевой функции в ЗЛП достигается в вершине (крайней, угловой точке).
 2014-02-12
2014-02-12 12727
12727
