Операции над множествами

Над множествами можно выполнять действия (операции), напоминающие сложение и умножение чисел. Но не тождественные им.

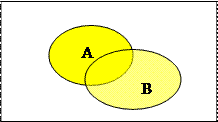
Объединением (суммой0 множеств А и В называется множество, обозначаемое через АÈВ, содержащее те и только те элементы, которые принадлежат множеству А или В.

Краткая запись: АÈВ = {x | xÎ A или хÎ В}.

Соответствующая диаграмма Эйлера – Венна:

	АÈВ- заштрихованная область

Пример: А = {2, 5, 7, 9}, В = {3, 5, 8, 9, 12}.

АÈВ = {2, 5, 7, 9 }È{3, 5, 8, 9, 12}= {2, 5, 7, 9, 3, 8, 12}.

Соответствующая диаграмма:

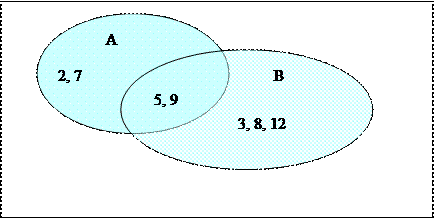
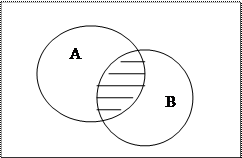
Пересечением (произведением) множеств А и В называется множество, обозначаемое через АÇВ и состоящее из тех и только из тех элементов, которые принадлежат множеству А и множеству В.

Краткая запись: АÇВ = {x | xÎA и хÎВ}.

Соответствующая диаграмма Эйлера- Венна:

АÇВ – заштрихованная область

Пример: АÇВ= {2, 5, 7, 9 }Ç{3, 5, 8, 9, 12}= {5,9}.

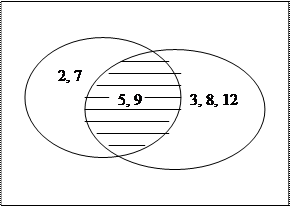Диаграмма:

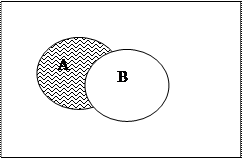
Разностью множеств А и В называется множество, обозначаемое через А\В и состоящее из тех и только из тех элементов, которые принадлежат А и не принадлежат В.

Краткая запись: А\В = {x| xÎ A и xÏB}.

Соответствующая диаграмма Эйлера- Венна:

		А\В- заштрихованная область

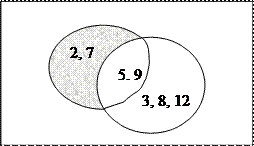
Пример: А\В = {2, 5, 7, 9 }\{3, 5, 8, 9, 12}= {2, 7}.

Диаграмма:

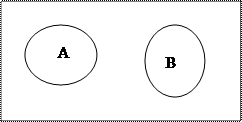
Если АÇВ = Æ, то А\В= А и В\А = В.

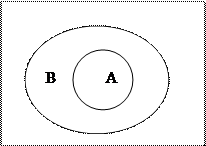
Если А Í В, то А\В = Æ.

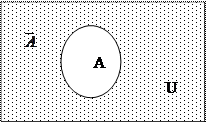Если U – универсальное множество и АÍ U, то разность U\A называется дополнением множества А до множества U и обозначается .

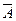Краткая запись: 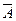= {x| xÎU и xÏA}.

Соответствующая диаграмма Эйлера- Венна:

Симметрической разностью множеств А и В называется множество, обозначаемое АDВ и состоящее из тех и только из тех элементов, которые принадлежат А\В или В\А.

Краткая запись: ADB= {x| xÎA\B или xÎB\A}.

Соответствующая диаграмма Эйлера- Венна:

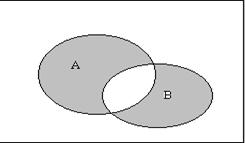
Пример: АDВ = {2, 5, 7, 9 }D{3, 5, 8, 9, 12}= {2, 7, 3, 8, 12}.

Диаграмма:

1 3 2

Пример: Найти множество: (АÇВ)D(С\Q), где:

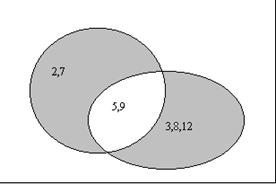
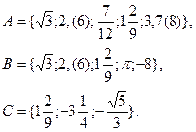
Расставим порядок действий и выполним их по порядку:

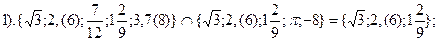
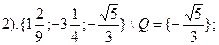
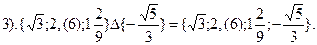
4. Алгебра множеств.

Непосредственной проверкой можно доказать справедливость следующих соотношений:

1. Коммутативность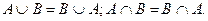

2. Ассоциативность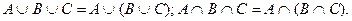

3. Дистрибутивность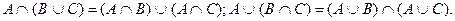

4. Закон поглощения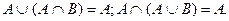

5. Закон де Моргана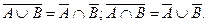

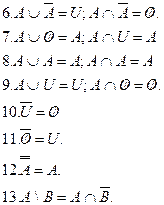
Приведенные выше соотношения называются тождествами алгебры множеств.

Заметим, что если в равенстве заменить È на Ç, U на Æ и наоборот, то получим справедливое равенство.

Этот закон называется принципом двойственности.

Докажем, например, справедливость равенства 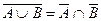аналитически и с помощью диаграмм Эйлера – Венна.

Пусть х Є АU В, что означает хÎU и хÏАÈВ. Отсюда следует, что хÏА и хÏВ, но тогда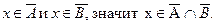

Построим диаграммы для обеих частей равенства и сравним их.

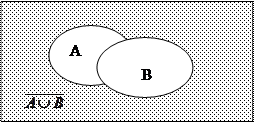Диаграмма для левой части:

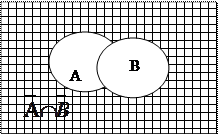Диаграмма для правой части:

Сравнивая диаграммы, убеждаемся в справедливости равенства.

Пользуясь тождествами можно производить преобразования над множественными выражениями и доказывать тождества.

Пример1: доказать тождество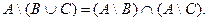

Рассмотрим два способа: с помощью диаграмм и тождеств.

1 способ

Левая часть тождества

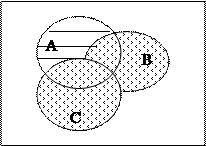
- результат

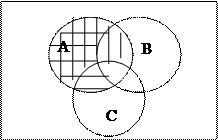Правая часть тождества

- результат

2 способ

Преобразуем левую часть тождества: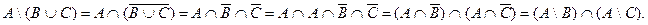

Тем самым доказали верность тождества.

Пример2: Доказать тождество: 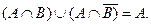Составить двойственное и тоже доказать.

Доказательство справедливости равенства и двойственного равенства с помощью диаграмм предлагаем выполнить самостоятельно.

Приведем доказательство справедливости данного равенства путем преобразований (доказательство для двойственного проведите самостоятельно):

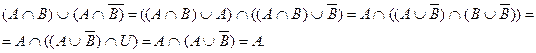
Пример3: Доказать тождество: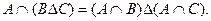

Преобразуем правую часть тождества:

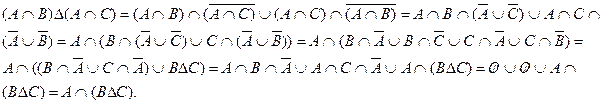
Тождество доказано.

5. Теорема о количестве подмножеств конечного множества.

Рассмотрим множество А = {1, 2, 3 }, где |A| = 3, и множество В = {5, 6, 7, 8}, где |B| = 4.

Составим всевозможные подмножества множества А:

А, Æ, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}.

Всего получили 8 подмножеств.

Составим всевозможные подмножества множества В:

В, Æ, {5}, {6}, {7}, {8}, {5,6}, {5,7}, {5,8}, {6,7}, {6,8}, {7,8}, {5,6,7}, {5,7,8}, {6,7,8}, {5,6,8}.

Получили 16 подмножеств.

Используя результаты рассмотренных примеров, можно предположить справедливость следующего равенства: n = 2^m, где n – количество подмножеств данного конечного множества, m – мощность множества.

Справедливость предположения подтверждает теорема, которую мы примем без доказательства.

Теорема: Если для конечного множества А его мощность равна т, то количество всех подмножеств данного множества, обозначаемое Р(А), равно 2^т.

Пример: Вычислить количество подмножеств множества М – делителей числа 20.

Составим множество М и найдем его мощность:

М = {1,2,4,5,10,20}. Мощность |M| = 6, тогда количество подмножеств равно Р(М) = 2⁶ = 64.

6. Формула включений и исключений.

Проиллюстрируем теперь применение операций над множест­вами для решения задач о нахождении числа элементов мно­жеств, заданных несколькими условиями. Ниже мы будем рас­сматривать только конечные множества.

Пример: В классе 30 учащихся, 16 из них занимаются му­зыкой, 17 увлекаются теннисом, а 10 занимаются и музыкой, и теннисом. Есть ли в классе ученики, равнодушные и к музыке, и к теннису, и если есть, то сколько их?

Решение: Если сложить число учащихся, интересующихся музыкой, с числом учащихся, занимающихся теннисом, т. е. 16+17=33, то учащиеся, интересующиеся и музыкой, и тенни­сом, окажутся учтенными дважды. Поэтому, чтобы определить число учащихся, интересующихся музыкой или теннисом, нужно из суммы 16+17 вычесть число учащихся, учтенных дважды, т. е. тех, кто интересуется и музыкой, и теннисом. По условию их 10. Таким образом, число интересующихся теннисом или музы­кой равно: 16+17—10=23 ученика. А так как в классе всего 30 учащихся, то 30—23 ==7 учащихся равнодушны и к музыке, и к теннису.

Задача решена по следующему алгоритму: пусть имеется два конечных множества А и В. Тогда:

п(АÈ В) = п(А) + п(В)- п(АÇ В) (1)

В нашем случае А — множество учащихся, интересующихся му­зыкой, и n(A) = 16, В— множество учащихся, интересующихся теннисом, и n(B) = 17, n(AÇB) =10, и тогда по полученной формуле n(AUВ)=16+17-10=23.

Усложним задачу: пусть к тем, кто интересуется в классе му­зыкой — множеству А, и к тем, кто увлекается теннисом — мно­жеству В, добавляются еще и те, кто интересуется театром— множество С. Сколько учеников увлекается или музыкой, или теннисом, или театром, т. е. чему равно число n{AÈ B È C)?

Если множества А, В и С пересекаются лишь попарно, т. е. АÇВÇС=Æ, то подсчет можно вести, как и прежде: снача­ла сложить п(А)+п(В)+п(С), а затем вычесть число тех эле­ментов, которые подсчитаны дважды, т. е. вычесть число n{AÇ B}+n(AÇ C)+n(BÇ C). Если же множество АÇВÇС¹Æ,, то его элементы оказались неучтенными: сначала их трижды учли, когда складывали п(А}+п (В)+п(С), а затем трижды отнимали их, вычитая n{AÇ B}+n(AÇ C)+n(BÇ C).

Таким об­разом, число

п(А)+п(В)+п(С)- (n{AÇ B}+n(AÇ C)+n(BÇ C))

меньше истинного результата ровно на число элементов в пере­сечении множеств АÇВÇС, которое и следует добавить для по­лучения верного результата:

п(А)+п(В)+п(С)- (n{AÇ B}+n(AÇ C)+n(BÇ C))+п(АÇ ВÇ С) (2)

Аналогичная формула может быть получена для любого числа множеств.

В формулах (1) и (2) подсчитывается, сколько раз каждый элемент включается и исключается, поэтому их называют фор­мулами включений и исключений.

Рассмотрим несколько примеров применения полученных формул.

Пример1: На вступительном экзамене по математике были предложены три задачи: по алгебре, планиметрии и стереометрии. Из 1000 абитуриентов задачу по алгебре решили 800, по планиметрии — 700, а по стереометрии — 600 абитуриентов. При этом задачи по алгебре и планиметрии решили 600 абитуриен­тов, по алгебре и стереометрии — 500, по планиметрии и стерео­метрии — 400. Все три задачи решили 300 абитуриентов. Суще­ствуют ли абитуриенты, не решившие ни одной задачи, и если да, то сколько их?

Решение. Пусть U — множество всех абитуриентов, А —. множество абитуриентов, решивших задачу по алгебре, В — множество абитуриентов, решивших задачу по планиметрии, С — множество абитуриентов, решивших задачу по стереометрии. По условию n(U) =1000, n(A) = 800, n(В)=700, n(С)=600, n(AÇB)= 600, n(AÇC) = 500, n(BÇC) = 400, n(AÇBÇC) =300. В множество AÇBÇC включены все абитуриенты, решившие хо­тя бы одну задачу. По формуле (2) имеем:

n(А U В U С) == 800 + 700 + 600 - 600 - 500 - 400 + 300 =900.

Отсюда следует, что не все поступающие решили хотя бы одну задачу. Ни одной задачи не решили

n(U) - n(AUBUC)=1000 - 900==100 (абитуриентов).

Пример2: Социологи опросили 45 учащихся девятых клас­сов, среди которых 25 юношей. При этом выяснилось: 30 человек имеют за полугодие оценки 4 и 5, из них 16 юношей, спортом занимаются 28 учеников, среди них 18 юношей, и 17 учеников, успевающих только на хорошо и отлично, 15 юношей учатся на хорошо и отлично и занимаются спортом. Первый математик класса взглянул на результаты и заявил, что там есть ошибки. Как это ему удалось выяснить?

Решение: Обозначим через А множество юношей, В — множество успевающих на 4 и 5, С — множество спортсменов. По условию задачи n(A)=25, n(В)=30, n(С)=28, n(AÇB)=16, n(AÇC)=18, n(BÇC)=17, n(AÇBÇC)=15. Найдем общее чис­ло учащихся, которые или являются юношами, или занимаются спортом, или успевают на 4 и 5. По формуле (2) получаем:

n (A UBUC)=25+30+28- 16- 18- 17+15=47. Этого быть не может, так как обследовалось всего 45 учеников! Следовательно, в данных сведениях есть ошибки.

На рисунке это решение проиллюстрировано с помощью диаграммы Эйлера — Венна.

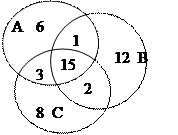В пересечении множеств А, В и С за­пишем число 15, так как по условию n(AÇBÇC)=15. В мно­жестве AÇB\С запишем число 16—15=1, в множестве BÇC\А - число 18-15=3, в множестве BÇC\А—число 17-15=2, в множестве A\(BÈC)— число 25-(1+15+3)=6, в множестве В\(А ÈC) — число 30-(1 + 15+2)= 12, в множест­ве С\(АÈВ)— число 28-(3+15+2)=8. Чтобы найти n(АÈВÈС), достаточно сложить записанные числа, поскольку они соответствуют множествам, не пересекающимся между со­бой. Получим число 47 > 45, что невозможно по условию задачи.

Задачи для самостоятельного решения

1. Опишите множество М точек на плоскости: a) {M| OM = R}; б) {M| OM£ R}; в) {M| AM = MB}.

2. Даны множества: 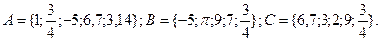Построить множество ((АDВ)È(В\С)). Найти количество подмножеств построенного множества. Показать соответствующую диаграмму Эйлера – Венна.

3. Доказать с помощью диаграмм Эйлера – Венна справедливость закона поглощения.

4. Доказать тождества с помощью диаграмм и путем преобразований: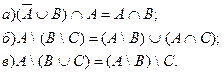

5. В отделе института работают несколько человек. Каждый из них знает хотя бы один иностранный язык, причем: 6 знают немецкий, 6 – английский, 7 – французский, 4 – английский и немецкий, 3 – немецкий и французский, 2 – французский и английский, 1 – все три языка. Сколько всего человек работает в отделе? Сколько из них знают только английский?

6. Из 35 учащихся класса 20 посещают математический кружок, 11 – физический, 10 – не посещают кружки. Сколько учеников посещают математический и физический кружки одновременно, сколько – только математический?

Контрольные вопросы

1. Объясните понятие множества. Приведите примеры множеств. Как обозначаются множества и их элементы?

2. Какие существуют способы задания множеств?

3. С помощью характеристического свойства задайте конечное, бесконечное несчетное, бесконечное счетное и пустое множества.

4. Как обозначается принадлежность элемента множеству и не принадлежность?

5. Какие существуют отношения между двумя множествами?

6. Перечислите операции над множествами с приведением соответствующих диаграмм Эйлера – Венна.

7. Перечислите тождества алгебры множеств.

8. Сформулируйте теорему о количестве подмножеств конечного множества.

9. Запишите формулы количества элементов в объединении двух и трех множеств.