Лекция 7
Контрольные вопросы
Приложения алгебры логики в технике (релейно-контактные схемы).
Среди технических средств автоматизации значительное место занимают устройства релейно-контактного действия. Они широко используются в технике автоматического управления, в электронно-вычислительной технике и т.д.
Эти устройства (их в общем случае называют переключательными схемами) содержат сотни реле, электронных ламп, полупроводников и электромагнитных элементов. Описание и конструирование таких схем в силу их громоздкости весьма затруднительно.
Еще в 1910 году физик П. С. Эренфест указал на возможность применения аппарата алгебры логики при исследовании релейно-контактных схем (РКС). Однако его идеи стали реализовываться значительно позже, когда создание общей теории конструирования РКС стало остро необходимым.
Использование алгебры логики в конструировании РКС оказалось возможным в связи с тем, что каждой схеме можно поставить в соответствие некоторую формулу алгебры логики, и каждая формула алгебры логики реализуется с помощью некоторой схемы.
Это обстоятельство позволяет выявить возможности заданной схемы, изучая соответствующую формулу, а упрощение схемы свести к упрощению формулы.
С другой стороны, до построения схемы можно заранее описать с помощью формулы те функции, которые схема должна выполнять.
Рассмотрим, как устанавливается связь между формулами алгебры логики и переключательными схемами.
Под переключательной схемой понимают схематическое изображение некоторого устройства, состоящего из следующих элементов:
1) переключателей, которыми могут быть механические действующие устройства (выключатели, переключающие ключи, кнопочные устройства и т. д.), электромагнитные реле, электронные лампы, полупроводниковые элементы и т.п.;
2) соединяющихих проводников;
3) входов в схему и выходов из нее (клемм, на которые подается электрическое напряжение). Они называются полюсами схемы.
Сопротивления, конденсаторы и т.д. на схемах не изображаются.
Переключательной схемой принимается в расчет только два состояния каждого переключателя, которые называют «замкнутым» и «разомкнутым».
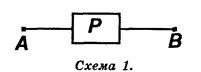
Рассмотрим простейшую схему, содержащую один переключатель Р и имеющую один вход А и один выход В. Переключателю Р поставим в соответствие высказывание р, гласящее: «Переключатель Р замкнут». Если ристинно, то импульс, поступающий на полюс А, может быть снят на полюсе В без потери напряжения. Будем в этом случае говорить, что схема проводит ток. Если рложно, то переключатель разомкнут, и схема тока не проводит или на полюсе В снимается минимальное напряжение при подаче на полюс А максимального напряжения.
Если принять во внимание не смысл высказывания, а только его значение, то можно считать, что любому высказыванию может быть поставлена в соответствие переключательная схема 1.
Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы.
Конъюнкция двух высказываний р v q будет представлена двухполюсной схемой с последовательным соединением двух переключателей Р и q (схема 2).
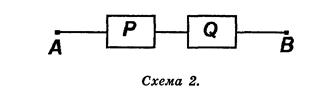
Эта схема пропускает ток тогда и только тогда, когда истинны высказывания р и q одновременно, то есть pqº 1.
Дизъюнкция двух высказываний рvqдвухполюсной схемой с параллельным соединением переключателей Р и Q (схема 3).
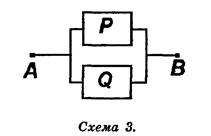
Эта схема пропускает ток в случае, если истинно высказывание р или истинно высказывание q, то есть р v q º 1.
Если высказывание 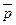 есть отрицание высказывания р, то тождественно истинная формула
есть отрицание высказывания р, то тождественно истинная формула 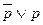 изображается схемой, которая проводит ток всегда (схема 4), а тождественно ложная формула р&
изображается схемой, которая проводит ток всегда (схема 4), а тождественно ложная формула р&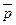 изобразится схемой, которая всегда разомкнута (схема 5).
изобразится схемой, которая всегда разомкнута (схема 5).
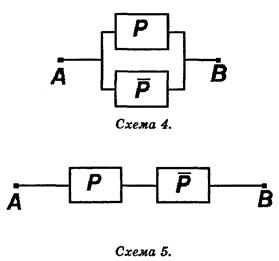
Из схем 1, 2 и 3 путем последовательного и параллельногоих соединения могут быть построены новые двухполюсные переключательные схемы, которые называют П-схемами.
Как было показано, всякая формула алгебры логики путем равносильных преобразований может быть представлена в виде формулы, содержащей только две операции: конъюнкцию и отрицание или дизъюнкцию и отрицание. Из этого следует, что всякая формула алгебры логики может быть изображена П-схемой и, обратно, для любой П-схемы может быть записана формула, которая изображается этой схемой.
Примеры.
1. Формуле 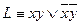 соответствует схема 6:
соответствует схема 6:
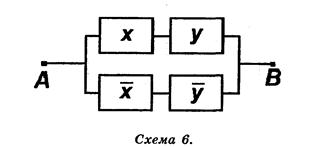
2.
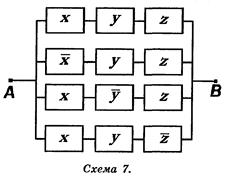
Для схемы 7 соответствующая формула алгебры логики имеет вид:
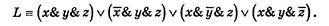
Упростим эту формулу следующим образом:
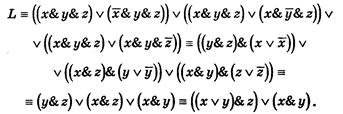
Последней формуле соответствует П-схема 8:
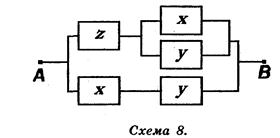
Из второго примера следует, что для некоторых РКС путем равносильных преобразований соответствующей формулы алгебры логики можно получить РКС, содержащую меньшее число переключателей. Проблема решения этой задачи носит название проблемы минимизации.
Приведем пример построения РКС по заданным условиям с оценкой числа контактов.
Построить контактную схему для оценки результатов некоторого спортивного соревнования тремя судьями при следующих условиях: судья, засчитывающий результат, нажимает имеющуюся в его распоряжении кнопку, а судья, не засчитывающий результат, кнопки не нажимает. В случае, если кнопки нажали не менее двух судей, должна загореться лампочка (положительное решение судей принято простым большинством голосов).
Работа нужной РКС описывается функцией Буля трех переменных F(x, у, z), где переменные высказывания х, у, z означают:
х - судья х голосует «за»,
у - судья у голосует «за»,
z - судья z голосует «за».
Таблица истинности функции F(x, у, z) имеет вид:
| х | y | z | F(x, у, z) |
Функции соответствует формула:
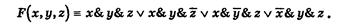
А этой формуле соответствует РКС, изображенная на схеме 7, которая содержит двенадцать переключателей.
Но как было показано, в результате равносильных преобразований формула F(x, у, z) может быть приведена к виду:
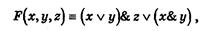
которому соответствует РКС, изображенная на схеме 8, содержащей пять переключателей.
Задачи для самостоятельного решения.
- По таблице истинности найти формулы, определяющие функции F1, F2.
| x | y | z | F1 | F2 |
2. Составьте формулу для булевой функции F(x,y,z) = 1, если а) только одна какая-либо переменная равна нулю; б) если большинство переменных равны нулю. Упростите полученные формулы.
3. Составить РКС для формул:
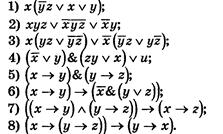
4. Построить схемы, реализующие следующие булевы операции:
- импликацию;
- эквиваленцию.
5. Построить РКС для функций, если известно, что:
- F(0,1,0)=F(1,0,1)=F(1,1,1)=1;
- F(1,0,1)=F(1,1,0)=1;
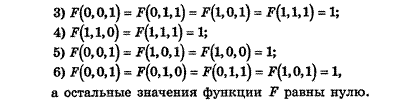 |
6. Упростить РКС:
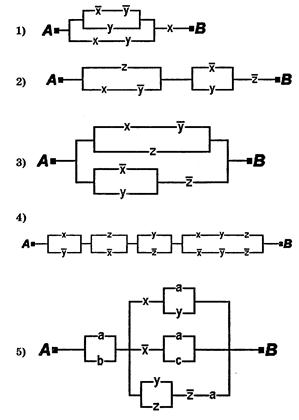 |
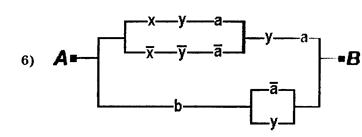 |
7. Проверить равносильность схем:
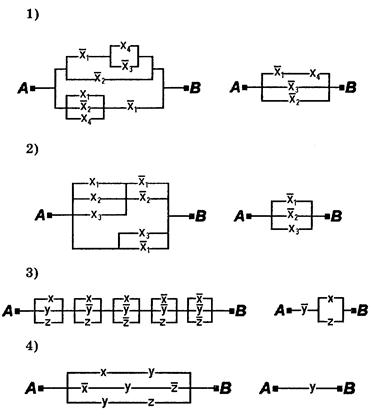 |
1. Какое множество называется алгеброй Буля?
2. Какие интерпретации алгебры Буля нам знакомы?
3. Определение функции алгебры логики.
4. Как представить заданную таблицей истинности функцию в виде формулы алгебры логики?
5. Что называется релейно-контактной схемой?
6. Какие виды соединений переключателей соответствуют основным логическим операциям?
7. Как нужно представить формулу, чтобы для нее можно было бы составить РКС?
ТЕМА: СОВЕРШЕННЫЕ НОРМАЛЬНЫЕ ФОРМЫ.
ПЛАН:
1. Совершенная дизъюнктивная нормальная форма.
2. Совершенная конъюнктивная нормальная форма.
Главная
1. Совершенная дизъюнктивная нормальная форма.
Формула, составленная для заданной таблицей истинности функции, по выше приведенному правилу обладает свойствами, которые называются свойствами совершенства. Перечислим их:
1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию.
2. Все логические слагаемые различны.
3. Ни одно слагаемое не содержит одновременно переменную и ее отрицание.
4. Ни одно слагаемое не содержит одну и ту же переменную дважды.
Каждой не тождественно ложной формуле соответствует единственная формула с такими свойствами.
Для одной и той же формулы можно составить множество равносильных ей ДНФ. Но среди них существует единственная ДНФ с перечисленными свойствами совершенства.
ДНФ, для которой выполняются свойства совершенства называется совершенной ДНФ (СДНФ).
Составленная формула по таблице истинности и является СДНФ формулы.
Если функция задана какой – либо формулой, то для получения СДНФ формулы необходимо составить таблицу истинности. Если формула содержит большое количество переменных высказываний, то этот способ практически не приемлем. В этом случае получают СДНФ формулы путем равносильных преобразований.
Приведем соответствующий алгоритм:
1. Путем равносильных преобразований получить какую – либо ДНФ.
2. Если какая-либо элементарная конъюнкция В не содержит переменную хi, то вводят ее, используя равносильность 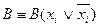 . И раскрывают скобки.
. И раскрывают скобки.
3. Если в ДНФ входят две одинаковые конъюнкции В, то лишнюю отбрасывают, используя свойство идемпотентности ВV B º B.
4. Если какая-либо конъюнкция содержит xi вместе с отрицанием, то В º 0. И В исключают из ДНФ.
5. Если какая-либо конъюнкция содержит переменную xi дважды, то одну из них отбрасывают, используя свойство xi xi º xi.
Примеры.
1. Составить СДНФ для формулы по таблице истинности и путем равносильных преобразований.
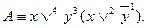
Составим таблицу истинности, которая содержит 4 строки.
| х | у | ||||
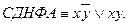
Получим какую-либо ДНФА и преобразованиями доведем до совершенства: 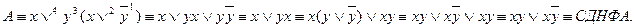
2. Аналогичное задание для формулы 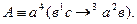
Составим таблицу истинности, содержащую 8 строк.
| a | b | c | ||||
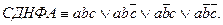
Преобразуем формулу: 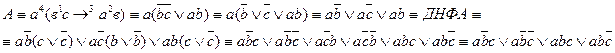
3. Путем равносильных преобразований получить СДНФА.
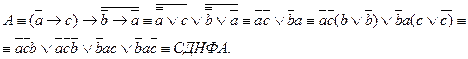
 2014-02-12
2014-02-12 6275
6275
