Любую булеву функцию моно представить в виде ДНФ или КНФ. Равносильными преобразованиями можно представить формулу с меньшим количеством переменных. Например:
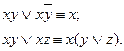
первое преобразование не выводит формулу из класса ДНФ, а последнее – выводит. Будем минимизировать формулы только в классе ДНФ.
ДНФ формулы А называется минимальной. Если она содержит наименьшее число вхождений переменных по сравнению с остальными ДНФ этой формулы.
Значит, минимальную ДНФ можно найти, перебрав все ДНФ. Но при большом количестве переменных этот способ практически не применим. Существуют эффективные способы нахождения минимальной ДНФ. Рассмотрим некоторые из них.
Первый из способов, на котором мы остановимся называется методом минимизирующих карт. Он может показаться громоздким, но преимущество этого способа в его простоте и возможности реализации на компьютере.
Булева функция должна быть задана таблицей истинности или какой –либо совершенной нормальной формой. Составляют карту, которая имеет вид:

далее используют утверждение:
если какая- либо конъюнкция, содержащая все переменные и принадлежащая j – той строке карты, не входит в СДНФ, выражающую функцию, то любая конъюнкция этой строки не входит ни в какую ДНФ, выражающую исходную функцию.
Опираясь на данное утверждение, получаем алгоритм построения минимальной ДНФ.
1. Отметим в карте строки, в которых конъюнкция (в последнем столбце) не принадлежит СДНФ формулы;
2. Вычеркнем все конъюнкции в этих строках и во всех остальных строках карты;
3. В каждой строке выберем из оставшихся конъюнкций конъюнкции с наименьшим числом переменных, остальные вычеркнем;
4. В каждой строке выберем по одному оставшемуся элементу и составим из них ДНФ;
5. Из всех составленных ДНФ выберем минимальную.
Пример: 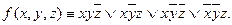 Составим карту:
Составим карту:
| x | y | z |  xy xy | xz | yz | xyz | - |
| x | y | 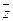 | xy | x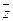 | y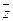 | xy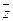 | + |
| x | 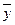 | z | x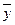 | xz | 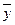 z z | x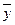 z z | + |
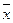 | y | z | 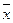 y y | 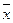 z z | yz | 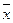 yz yz | - |
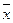 | y | 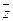 | 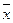 y y | 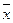 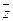 | y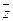 | 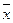 y y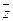 | - |
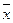 | 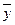 | z | 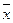 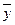 | 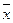 z z | 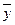 z z | 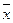 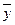 z z | + |
| х | 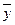 | 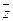 | x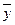 | x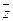 | 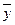 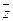 | x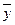 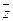 | + |
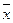 | 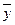 | 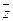 | 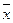 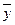 | 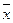 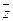 | 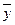 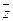 | 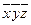 | - |
Вычеркнем конъюнкции, отсутствующие в формуле и соответствующие строки. Вычеркнутые конъюнкции вычеркнуть и в остальных строках.
Составим всевозможные ДНФА, выбирая из каждой строки по одной оставшейся конъюнкции:
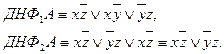
ДНФ2А является минимальной.
 2014-02-12
2014-02-12 3854
3854
