2014-02-12
1041
Данный метод минимизации основан на применении свойства идемпотентности, поглощения и склеивания.
Рассмотрим этот метод на примере. Пусть заданы номера наборов из 4-х переменных, на которых функция равна единице: f(2,5,6,7,10,12,13,14) = 1. Необходимо составить СДНФ:
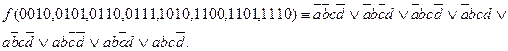
Далее упростить формулу, применив закон склеивания и идемпотентности, получим:
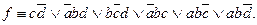
Теперь составим таблицу Квайна: по вертикали перечислены все элементарные конъюнкции, вошедшие в последнюю ДНФ, по горизонтали - элементарные конъюнкции, входящие в СДНФ. Единица в ячейке ставится, если конъюнкция ДНФ «накрывает» (используя закон поглощения) конъюнкцию в СДНФ. В каждом столбце оставляют по одной единице, исключая избыточные. Выбор единиц производят из соображения минимальности множителей в конъюнкции. Покажем таблицу:
| abcd |  |  |  |  |  |  |  |  |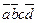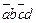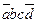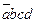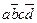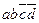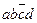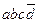
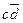 | 1V | 1V | 1V | 1V | ||||
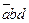 | 1V | 1V | ||||||
 | ||||||||
 | ||||||||
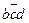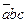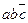 | 1V | 1V | ||||||
 |
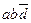Выбранные ячейки отметим знаком «V». На последнем этапе минимизации получаем ДНФ: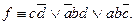 
Отметим, что в общем случае решений может быть несколько.
