Обозначим через Еn множество всех наборов 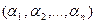 из 0 и 1. Это множество будем рассматривать как множество всех вершин единичного n –мерного куба. Само множество Еn будем называть единичным n – мерным кубом. Количество вершин куба Еn равно 2n.
из 0 и 1. Это множество будем рассматривать как множество всех вершин единичного n –мерного куба. Само множество Еn будем называть единичным n – мерным кубом. Количество вершин куба Еn равно 2n.
0-мерный куб – это одна вершина или точка.
Одномерный куб – Е1, множество вершин {(0), (1)}:

Двухмерный куб – Е2, множество вершин {(00), (01), (10), (11)}:

 Трехмерный куб – Е3, множество вершин {(000), (001), (010), (001), (110), (011), (101), (111)}:
Трехмерный куб – Е3, множество вершин {(000), (001), (010), (001), (110), (011), (101), (111)}:
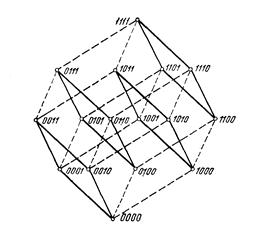
Четырехмерный единичный куб – Е4:
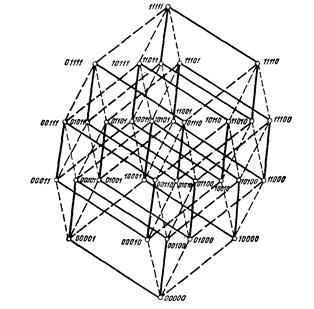
Пятимерный единичный куб – Е5:
Заметим, что наборы, соответствующие соседним вершинам куба, т.е. вершинам, которые соединяются ребром, отличаются значением только какой –либо одной координаты, как соседние ячейки карты Карно.
Далее введем понятие грани куба.
Пусть si1, si2, si3,…, sir фиксированная система чисел из 0 и 1 такая, что 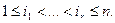 Множество всех вершин куба Еп таких, что ai1= si1, ai2 =si2, ai3= si3,…, air= sir называется (n –r) – мерной гранью.
Множество всех вершин куба Еп таких, что ai1= si1, ai2 =si2, ai3= si3,…, air= sir называется (n –r) – мерной гранью.
Введем в рассмотрение множество Nf всех вершин куба 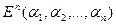 таких, что
таких, что 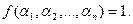 По этому множеству можно однозначно восстановить саму функцию.
По этому множеству можно однозначно восстановить саму функцию.
Пример: Функции f(x, y, z) соответствует множество Nf = {(000), (100), (101), (110), (111)}.
По данному множеству восстановим булеву функцию: 
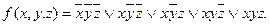
Графическое представление множества Nf:

Рассмотрим какую –либо элементарную конъюнкцию К из ДНФ функции n –переменных, состоящую из r множителей. Сопоставим ей множество таких наборов, при которых эта конъюнкция равна 1. Обозначим это множество Nk. Полученное таким образом множество называется (n –r) –мерной гранью куба Еn. Количество множителей – r в конъюнкции называется ее рангом. Ранг конъюнкции является и рангом соответствующей грани.
Пример: Дана ДНФ каrой-либо фукнции f(x, y, z): 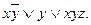
Составим для каждой конъюнкции множество Nki:
Nk1= {(100), (101)} – это 3-2=1 – одномерная грань трехмерного куба, ранг равен 2;
Nk2= {(010), (110), (011), (111)} – это 3-1 = 2 – одномерная грань трехмерного куба, ранг - 1;
Nk3= {(011)} – это 3-3=0 – нольмерная грань трехмерного куба, ранг -3.
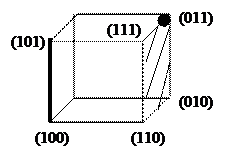
Легко заметить, что чем меньше ранг конъюнкции. Тем больше мерность соответствующей грани.
Свойства соответствия между f и Nf:
Если f(x1, x2, …, xn) = g(x1, x2, …, xn)Vh(x1, x2, …, xn), то:
1. Ng Í Nf, Nh Í Nf;
2. Nf = Ng È Nh.
В частности следует. Что если f – есть ДНФ: f = К1V К2 V…VКs, то из указанных свойств следут, что Nki Í Nf, т.е. Nki – это грань расположенная внутри множества Nf и:
Nf = Nk1È Nk2 È…ÈNks, т.е. множество Nf покрывается гранями Nk1, Nk2 ,…,Nks.
Если грани Nki имеют ранги ri (i = 1-s), то ранг всего покрытия равен 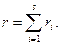
Теперь сформулируем задачу минимизации в геометрической форме (задача о покрытии):
Найти для данного множества Nf такое покрытие гранями Nki, чтобы его ранг был наименьшим.
Пример: 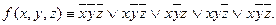
Составим множество Nf ={(000), (100), (101), (110), (100)}
Данное множество имеет точечное покрытие, соответствующее СДНФ, состоящее из 5 нольмерных граней. Используя закон склеивания можно минимизировать СДНФ. Графически эту задачу можно решить так: объединить вершины из множества Nf по возможности в грани большей мерности, а значит меньшего ранга. Покажем это на рисунке:
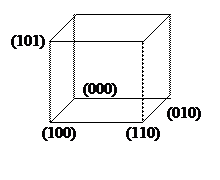 |
Вершины нижнего основания можно объединить в одну двухмерную грань {(100), (110), (010), (000)}, которой соответствует конъюнкция 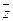 ; соседние вершины (100) и (101) соединим в одну одномерную грань {(100), (101)}, которой соответствует конъюнкция
; соседние вершины (100) и (101) соединим в одну одномерную грань {(100), (101)}, которой соответствует конъюнкция 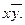
Значит, данное множество имеет еще одно покрытие одной двухмерной и одной одномерной гранями, а СДНФ равносильна ДНФ: 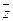 v
v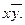
 2014-02-12
2014-02-12 2889
2889








