Сокращенная ДНФ

Познакомимся с сопутствующими понятиями.

Максимальная грань: N_k называется максимальной гранью, если не существует N_k’ такая, что:

1. N_k ÍN_f ÍN_k’;

2. размерность грани N_k’ больше размерности N_k.

Пример:

для каждой конъюнкции найдем грани и выявим максимальные:

N_k1 ={(000), (100)}- одномерная, максимальная,

N_k2 ={(100), (101)}- одномерная, является подмножеством N_k3, или, покрывается гранью N_k3, поэтому не является максимальной.

N_k3 ={(100), (110), (101), (111)}- двухмерная, максимальная.

Конъюнкции, соответствующие максимальным граням, называются простыми импликантами.

В нашем примере простыми импликантами будут К₁ и К₃.

ДНФ, являющаяся дизъюнкцией всех простых импликант функции f, называется сокращенной ДНФ.

Алгоритм построения сокращенной ДНФ:

1. составить какую-либо КНФ функции (можно СКНФ);

2. раскрыть скобки;

3. удалить нулевые члены, поглащаемые и дублирующие, т.е. К₁К₂VK₁º K₁, K₁VK₁º K₁.

Полученная ДНФ состоит только из простых импликант и является сокращенной.

Пример: Для функции 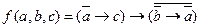построить сокращенную ДНФ.

Путем равносильных преобразований составим какую-либо КНФ и, выполняя пункты 2 и 3 алгоритма, получим сокращенную ДНФ:

Найдем грани конъюнкций:

N_k1 = {(000), (010)}- одномерная, максимальная,

N_k2 = {(100), (101)}- одномерная, максимальная,

N_k3 = {(000), (100)}- одномерная, максимальная.

Соответствующий рисунок: