Использование метода математической индукции для нахождения сумм конечного числа слагаемых

Этот метод можно эффективно использовать для нахождения формул вычисления сумм, когда число слагаемых зависит от n,доказательства тождеств, доказательства неравенств, у которых одна или обе части зависят от n.

Пример 1. Пусть дана последовательность (n)натуральных чисел. Найдем формулу вычисления суммы первых nчисел:

S(n)=l+2 + 3 +... + n.

Решение. Рассмотрим S(1), S(2), S(3), S(4). Мы имеем:

S(l)=l,

S(2)=1+2 = 3,

S(3)=1+2 + 3 = 6,

S(4)=1+2 + 3 + 4=10.

Заметив, что полученные числа можно записать в виде

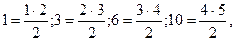
естественно сделать предположение, что

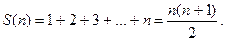(1)

Применим теперь метод математической индукции для доказа­тельства полученной формулы (1).

При n = 1: S(1) = 1×2/2=1.

Формула верна при n = 1. Предположим, что формула верна при n = k > 1:

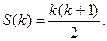
Тогда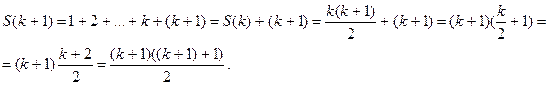

'Значит, из справедливости формулы для n = k вытекает ее справедливость для n = k + 1По принципу математической индукции отсюда вытекает справедливость формулы (1) для всех натуральных значений n.

В некоторых случаях для доказательства тождества Р(n) = Q (n)можем сначала убедиться, что Р (1) = Q (1), и, предпола­гая справедливость равенства P(k)=Q(k),k>1,доказать тож­дество P(k + 1) = Q(k + 1). Тогда из истинности равенства P(k) = Q(k) будет следовать истинность равенства P(k + 1) = Q(k + 1)и по принципу математической индукции бу­дет следовать истинность тождества P(n)=Q(n)для всех n.

Пример 2. Рассмотрим последовательность (n²) квадратов натуральных чисел. Докажем справедливость формулы для вы­числения суммы первых nчленов этой последовательности:

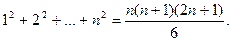(2)

Обозначим l² + 2² + 3² +... + n² = S (n)и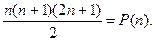

При n = 1: S(1) = 1, 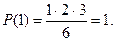Т.е. S(1) = P(1).

Предполагаем теперь, что равенство верно для n = k, k > 1, т. е. S(k) = P(k).

Рассмотрим разности:

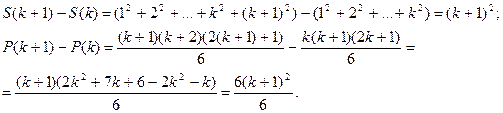
Итак, мы доказали, что S(1) = P(1) и S(k+l) - S (k) = = P (k+1) - P (k).Тогда по принципу математической индукции тождество (2) справедливо для всех n.

Ранее доказанные формулы могут служить источником полу­чения новых формул.

Пример 3. Пусть дана последовательность (n³)кубов нату­ральных чисел. Выведем формулу для вычисления суммы пер­вых nчленов этой последовательности:

S(n)=l³ + 2³ + 3³ + … + n³.

Как и в примере 1, рассмотрим суммы S(1), S (2), S (3), S (4). Здесь мы имеем:

S(l)=l,

S(2)=l³ + 2³ = 9,

S(3)=l³ + 2³ + 3³ = 36,

S (4)= 1³ + 2³ + 3³ + 4³= 100.

Поскольку мы предполагали, что S(k) = P(k),то отсюда сле­дует равенство S (k+ 1) = P (k + 1). Следовательно, по принципу математической индукции формула (3) справедлива для всех n.