Задачи для самостоятельного решения. 1. Доказать несправедливость утверждений

1. Доказать несправедливость утверждений:

а) «Если дифференцируемая функция у= f(x) имеет в точке х₀ вторую производную, равную нулю, то точка х₀ – точка перегиба графика функции».

б) «Если числовая последовательность ограничена, то она имеет предел».

в) «Если функция непрерывна в точке х₀, то она имеет производную в этой точке».

2. Для каждого из условий выясните, является ли оно необходимым и является ли оно достаточным, чтобы выполнялось неравенство х² – 3х – 18 £ 0: а) х=1, б) -2£ х £5, в) х³ -3, г) х> -3, д) -1£ х £ 10, е) –3 £ х £ 6.

3. Запишите на языке логики предикатов определение: «Функция f(x) называется ограниченной на множестве М, если существует такое неотрицательное число L, что для всех х ÎМ, справедливо неравенство |f(x)|£ M.»

4. В предложениях вместо многоточия поставьте слова «необходимо, но не достаточно», «достаточно, но не необходимо», «не необходимо и недостаточно», «необходимо и достаточно»:

а) Для того, чтобы четырехугольник был прямоугольным…, чтобы длины его диагоналей были равны;

б) Для того, чтобы х2 – 5х + 6 = 0…, чтобы х=3;

в) Для того, чтобы сумма четного числа натуральных чисел была четным числом…, чтобы каждое слагаемое было четным;

г) Для того, чтобы окружность можно было вписать в четырехугольник…, чтобы сумма длин суммы длин его противоположных сторон были равны;

д) Для того, чтобы множество было счетным…, чтобы его элементы можно было записать в виде занумерованной последовательности;

е) Для того, чтобы числовая последовательность имела предел…, чтобы она была ограниченной.

5.Сформулируйте:

а) Необходимый, но недостаточный признак параллелограмма;

б) Необходимый и достаточный признак параллелограмма;

в) Достаточное, но не необходимое условие, чтобы уравнение sinx = a имело решение.

г) Необходимое, но не достаточное условие, чтобы уравнение sinx = a имело решение.

Контрольные вопросы

1. Записать в виде формулы логики предикатов определение: а) непрерывности функции в точке; б) предела числовой последовательности; в) ограниченной функции.

2. Как выполняется построение противоположного утверждения к утверждению, заданному в виде формулы логики предикатов? Постройте противоположные утверждения для утверждений из первого пункта контрольных вопросов.

3. Приведите четыре вида теорем и объясните смысл каждой из них.

4. Какие из теорем являются равносильными?

5. Каким должно быть отношение между областями истинности предикатов Р(х) и Q(x), чтобы теорема 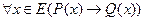была истинной? Какой в этом случае из предикатов необходимое и какой достаточное условие?

6. Какое отношение должно быть между областями истинности предикатов Р(х) и Q(x), чтобы для теоремы 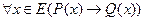была справедлива и обратная теорема? Какой теоремой можно заменить в этом случае прямую и обратную?

7. Докажите равносильность формул 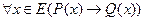и .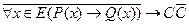

ЛЕКЦИЯ 14

ТЕМА: МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ

1. Понятие индукции. Аксиома математической индукции.

2. Использование метода математической индукции для нахождения сумм конечного числа слагаемых

3. Использование метода математической индукции для доказательства неравенств и делимости выражений, зависящих от n на некоторое число

4. Обобщение метода математической индукции

Главная

1. Понятие индукции. Аксиома математической индукции

Все утверждения можно разделить на общие и частные. На­пример, утверждение «Во всяком параллелограмме диагонали делятся в точке пересечения пополам» является общим, так как относится ко всему множеству параллелограммов. В то же время утверждение «В параллелограмме ABCD диагонали в точке пе­ресечения делятся пополам» является частным утверждением, так как относится к конкретному параллелограмму ABCD.

На основе частных утверждений делают некоторые предполо­жения (гипотезы) о справедливости какого-либо общего утверж­дения. Иногда эти предположения оказываются верными, иногда неверными. Переход от частных утверждений к общим называют индукцией (от латинского слова inductio — наведение). Напри­мер, знаменитый математик XVII в. П. Ферма, проверив, что

числа

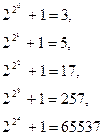
простые, сделал по индукции предположение, что для всех п = 1, 2,... числа вида 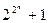- простые. Однако это предполо­жение оказалось неверным, так как в XVIII в. Л. Эйлер нашел, что 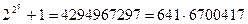— составное число. Как видим, индукция не является методом доказательства, а лишь помогает сформулировать неизвестный результат в виде некото­рой гипотезы, справедливость которой потом надо доказать.

В случае, когда утверждение касается конечного числа объектов, его можно доказать, проверяя для каждого объекта. Например, утверждение «Каждое чет­ное однозначное число является суммой двух простых чисел» легко проверить, рассмотрев равенства 2=1 + 1, 4 = 3+1, 6 = 5+1, 8 = 3 + 5.

Метод доказательства, при котором утверждение проверяется для каждого из конечного числа случаев, называют полной индукцией. Если же утверждение проверяется лишь для некоторых случаев и по индукции делается заключение о его справедливости для всех случаев, то индукцию называют неполной.

Индуктивные гипотезы формулируются обычно в виде утвер­ждений, относящихся ко всем натуральным числам. Последова­тельная проверка такого утверждения для каждого натурально­го числа п, начиная с 1, разумеется, невозможна, если говорить обо всех натуральных числах. Но сама идея последовательного перехода от натурального числа п к следующему за ним числу n +1 осуществляется в строгой форме в одном из самых важных методов математических доказательств, называемом методом математической индукции. В основе этого метода лежит аксиома индукции:

Предположение, что Р (n)справедливо для всякого натурального n, если:

1) оно справедливо для n =1;

2) из справедливости утверждения для какого-либо произ­вольного натурального n = kследует его справедливость для n = k +1.

Действительно, из того, что утверждение верно при n = 1, вы­текает по второму условию его справедливость для n = 1 + 1 = 2, но тогда оно верно и для n = 2 + 1=3, n = 3+1= 4 и т. д. Ясно, что в конце концов мы дойдем до любого натурального числа n.

Сам метод математической индукции состоит в следующем:

Для доказательства справедливости P(n) для любого n (P(n) – есть одноместный предикат от n, значит, доказываем "nP(n) º 1)

1. проверить истинность при n = 1, т.е. Р(1) = 1(истина);

2. допускают, что Р(n) = 1 при n = k и

3. проверяют истинность для n = k + 1.

Если P(k + 1) = 1, то "nP(n) º 1.