Определение 1.4.1. Полином 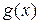 называется общим делителем двух полиномов
называется общим делителем двух полиномов 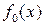 и
и 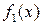 , если
, если 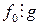 ,
, 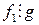 .
.
Определение 1.4.2. Общий делитель 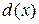 полиномов
полиномов 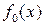 и
и 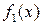 называется наибольшим общим делителем (НОД), если
называется наибольшим общим делителем (НОД), если 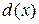 делится нацело на любой другой общий делитель этих полиномов.
делится нацело на любой другой общий делитель этих полиномов.
Определение 1.4.3. Полиномы 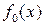 и
и 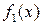 называются взаимно простыми, если они не имеют общих делителей положительных степеней.
называются взаимно простыми, если они не имеют общих делителей положительных степеней.
Лемма 1.4.1. Наибольший общий делитель двух полиномов определяется с точностью до постоянного сомножителя.
Доказательство. Пусть даны два различных наибольших общих делителя 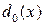 и
и 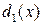 полиномов
полиномов 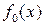 и
и 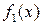 . По определению НОД имеем
. По определению НОД имеем
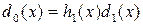 ,
,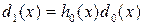
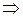
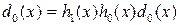
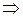
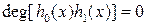
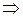
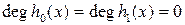 ,
,
т. е. полиномы 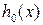 и
и 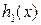 являются константами.
являются константами.
Приведем конструктивный способ построения НОД двух полиномов 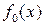 и
и 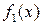 , который называется алгоритмом Евклида.
, который называется алгоритмом Евклида.
Пусть для определенности 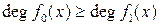 . Имеем цепочку равенств
. Имеем цепочку равенств
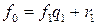 ,
, 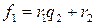 ,
, 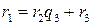 , …,
, …, 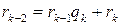 ,
, 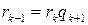 . (1.4.1)
. (1.4.1)
Так как 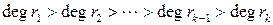 , то цепочка равенств (1.4.1) конечна и в ней существует звено, в котором деление осуществляется нацело. Докажем, что полином
, то цепочка равенств (1.4.1) конечна и в ней существует звено, в котором деление осуществляется нацело. Докажем, что полином 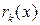 является наибольшим общим делителем полиномов
является наибольшим общим делителем полиномов 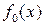 и
и 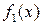 .
.
Действительно,
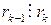
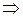
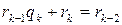
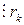
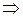
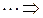
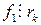 ,
, 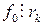 ,
,
т. е. 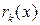 является общим делителем полиномов
является общим делителем полиномов 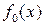 и
и 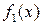 .
.
Пусть 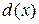 =НОД(
=НОД(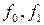 ).
).
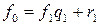
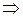
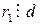 ,
, 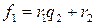
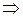
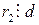 , …,
, …, 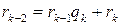
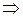
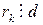 .
.
В силу произвольности 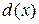 и в соответствии с определением НОД получаем, что
и в соответствии с определением НОД получаем, что 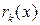 = НОД(
= НОД(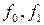 ).
).
Теорема 1.4.1. Если 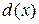 — это наибольший общий делитель полиномов
— это наибольший общий делитель полиномов 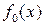 и
и 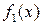 , то существуют такие полиномы
, то существуют такие полиномы 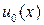 и
и 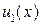 , что
, что
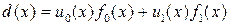 . (1.4.2)
. (1.4.2)
Доказательство. В соответствии с алгоритмом Евклида 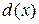 =
=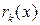 . Но
. Но
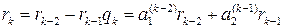 ,
,
где 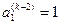 ,
, 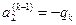 .
.
Из (1.4.1) 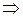
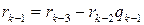
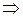
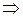
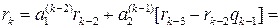
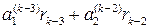 ,
,
где 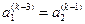 ,
, 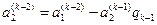 .
.
Далее заменяем 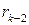 и т. д. В итоге имеем
и т. д. В итоге имеем
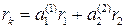 ,
,
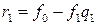 ,
, 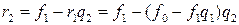 ,
,
Поэтому окончательно
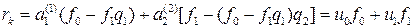 ,
,
где 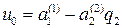 ,
, 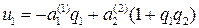 .
.
Следствие 1.4.1. Полиномы 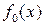 и
и 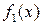 взаимно просты тогда и только тогда, когда существуют полиномы
взаимно просты тогда и только тогда, когда существуют полиномы 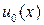 и
и 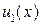 , для которых
, для которых
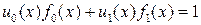 . (1.4.3)
. (1.4.3)
Следствие 1.4.2. Если НОД(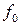 ,
,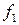 ) = 1, НОД(
) = 1, НОД(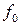 ,
,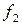 ) = 1, то
) = 1, то
НОД(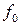 ,
,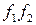 ) = 1.
) = 1.
Доказательство. Так как 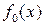 и
и 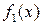 взаимно просты, то существуют такие полиномы
взаимно просты, то существуют такие полиномы 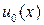 и
и 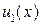 , что
, что
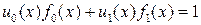 .
.
Умножая обе части данного соотношения на 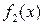 , получаем
, получаем
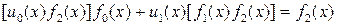 .
.
Пусть 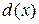 = НОД(
= НОД(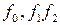 ),
), 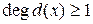 . Тогда
. Тогда
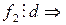 НОД(f 0, f 2) ¹ 1
НОД(f 0, f 2) ¹ 1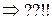
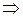 НОД(
НОД(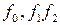 ) = 1.
) = 1.
Следствие 1.4.3. Если НОД(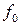 ,
,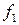 ) = 1, а
) = 1, а 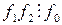 , то
, то 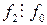 .
.
Доказательство. Поскольку 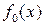 и
и 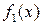 взаимно просты, то существуют такие полиномы
взаимно просты, то существуют такие полиномы 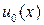 и
и 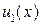 , что справедливо (1.4.3). Умножая обе части соотношения (1.4.3) на
, что справедливо (1.4.3). Умножая обе части соотношения (1.4.3) на 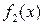 , получаем
, получаем
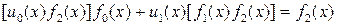 .
.
Левая часть данного равенства, очевидно, делится нацело на 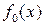 . Следовательно, делится нацело и правая часть, т. е.
. Следовательно, делится нацело и правая часть, т. е. 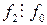 .
.
 2014-02-09
2014-02-09 605
605







