Лемма 1.5.1. Для произвольного полинома 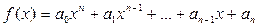 с вещественными коэффициентами и любого комплексного числа α справедливо равенство
с вещественными коэффициентами и любого комплексного числа α справедливо равенство 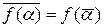 .
.
Доказательство. Пусть 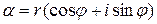 . Тогда по формуле Муавра
. Тогда по формуле Муавра
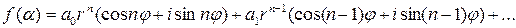
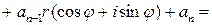
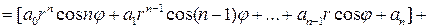
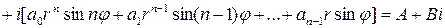 .
.
Очевидно, что
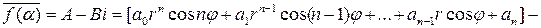
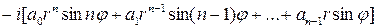 .
.
Так как 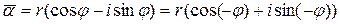 , то с учетом нечетности синуса и четности косинуса получаем
, то с учетом нечетности синуса и четности косинуса получаем
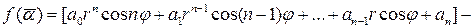
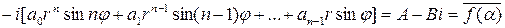 .
.
Определение 1.5.1. Полином с вещественными коэффициентами называется неприводимым, если он не делится нацело на полином с вещественными коэффициентами меньшей степени.
Теорема 1.5.1. Любой полином 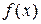 с вещественными коэффициентами однозначно с точностью до порядка сомножителей представляется в виде произведения неприводимых полиномов.
с вещественными коэффициентами однозначно с точностью до порядка сомножителей представляется в виде произведения неприводимых полиномов.
Доказательство. Пусть 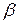 — произвольный комплексный корень полинома с вещественными коэффициентами
— произвольный комплексный корень полинома с вещественными коэффициентами 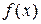 . Тогда
. Тогда
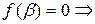
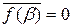
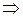
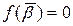 .
.
Таким образом, если комплексное число является корнем полинома с вещественными коэффициентами, то корнем является и комплексно сопряженное число.
Из теоремы 1.3.2 следует, что полином 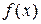 можно разложить на множители
можно разложить на множители
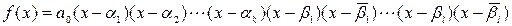 ,
,
где  — все вещественные корни полинома
— все вещественные корни полинома 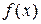 .
.
Ясно, что 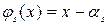 ,
, 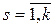 — это неприводимые полиномы.
— это неприводимые полиномы.
Рассмотрим полином
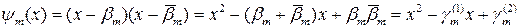 .
.
В силу свойств комплексных чисел 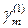 и
и 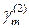 — это вещественные числа, поэтому полиномы
— это вещественные числа, поэтому полиномы 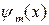 ,
, 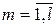 неприводимы.
неприводимы.
Доказанная теорема позволяет утверждать, что в общем случае, когда у полинома 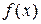 имеются кратные корни, то этот полином представляется в виде
имеются кратные корни, то этот полином представляется в виде
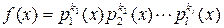 , (1.5.1)
, (1.5.1)
где 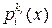 степень неприводимого полинома
степень неприводимого полинома  , причем
, причем 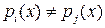 , когда
, когда 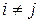 .
.
Теорема 1.5.2 (теорема Виета). Пусть 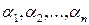 — корни приведенного полинома
— корни приведенного полинома 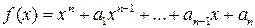 . Тогда между коэффициентами этого полинома и его корнями существуют следующие зависимости:
. Тогда между коэффициентами этого полинома и его корнями существуют следующие зависимости:
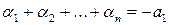 ,
,
 ,
,
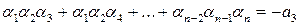 ,
,
…………
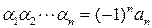 .
.
Доказательство. Доказательство проведем методом математической индукции. При 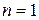 формулы очевидны, а при
формулы очевидны, а при 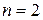 превращаются в хорошо знакомые формулы Виета для квадратного трехчлена. Допустим, что формулы справедливы при
превращаются в хорошо знакомые формулы Виета для квадратного трехчлена. Допустим, что формулы справедливы при 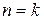 . Докажем их справедливость для случая
. Докажем их справедливость для случая 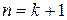 .
.
В силу индукционного предположения любой полином k– й степени, имеющий корни  , представим в виде
, представим в виде
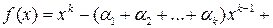
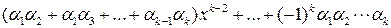 .
.
Если 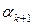 корень полинома степени
корень полинома степени 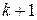 , то для этого полинома справедливо:
, то для этого полинома справедливо:
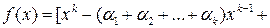
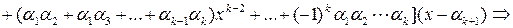
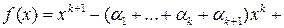
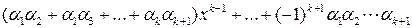 .
.
 2014-02-09
2014-02-09 1765
1765








