Определение 1.6.1. Рациональной дробью называется отношение двух полиномов с вещественными коэффициентами 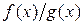 , где полином
, где полином 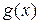 тождественно не равен нулю.
тождественно не равен нулю.
Определение 1.6.2. Рациональная дробь называется несократимой, если полиномы 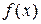 и
и 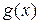 взаимно просты.
взаимно просты.
Определение 1.6.3. Рациональная дробь 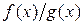 называется правильной, если
называется правильной, если 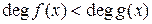 .
.
Добавим к множеству всевозможных правильных рациональных дробей число 0.
Теорема 1.6.1. Любая рациональная дробь однозначно представляется в виде суммы полинома и правильной дроби.
Доказательство. Если 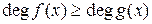 , то
, то
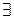
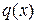 ,
,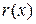 :
: 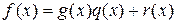 ,
,
где 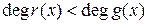 . Следовательно
. Следовательно
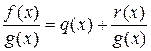 ,
,
причем 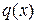 — полином, а
— полином, а 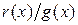 — правильная дробь.
— правильная дробь.
Определение 1.6.4. Правильная дробь 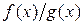 называется простейшей, если ее знаменатель
называется простейшей, если ее знаменатель 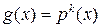 , где
, где 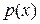 — неприводимый полином.
— неприводимый полином.
Теорема 1.6.2. Любая правильная рациональная дробь однозначно с точностью до порядка слагаемых разлагается в сумму простейших дробей.
Доказательство. Рассмотрим сначала правильную несократимую рациональную дробь
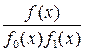 , (1.6.1)
, (1.6.1)
где НОД(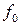 ,
,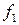 ) = 1. В силу следствия 1.4.1
) = 1. В силу следствия 1.4.1 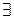
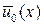 и
и 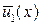 , что
, что
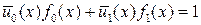 .
.
Умножая обе части этого равенства на полином 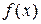 , получаем
, получаем
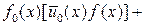
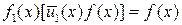 . (1.6.2)
. (1.6.2)
Представим полином 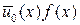 в виде
в виде 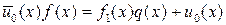 , где
, где 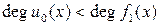 , и подставим его в соотношение (1.6.2). Тогда
, и подставим его в соотношение (1.6.2). Тогда
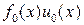
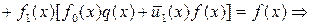
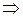
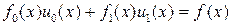 , (1.6.3)
, (1.6.3)
где 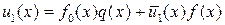 .
.
Дробь (1.6.1) является правильной, следовательно,
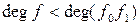 .
.
По построению 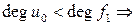
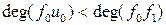 .
.
Из соотношения (1.6.3) имеем
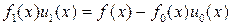
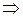
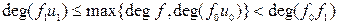 . Если разделить обе части соотношения (1.6.3) на произведение
. Если разделить обе части соотношения (1.6.3) на произведение 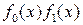 , то
, то
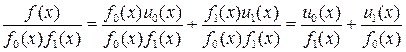 .
.
Таким образом, показали, что исходная несократимая правильная рациональная дробь (1.6.1) представима в виде суммы правильных дробей.
В силу формулы (1.5.1) полиномы 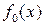 и
и 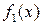 можно представить в виде произведения степеней неприводимых, а значит, взаимно простых полиномов. Поэтому дробь (1.6.1) допускает однозначное разложение в сумму правильных дробей
можно представить в виде произведения степеней неприводимых, а значит, взаимно простых полиномов. Поэтому дробь (1.6.1) допускает однозначное разложение в сумму правильных дробей
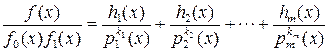 , (1.6.4)
, (1.6.4)
где 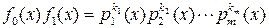 , причем
, причем 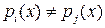 , когда
, когда 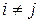 .
.
Рассмотрим теперь отдельно, например, первую дробь из правой части соотношения (1.6.4). Разделим 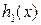 на полином
на полином 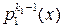 с остатком, а затем полученный остаток делим на полином
с остатком, а затем полученный остаток делим на полином 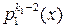 и т. д. В итоге получаем цепочку равенств:
и т. д. В итоге получаем цепочку равенств:
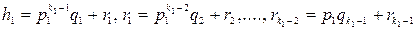 .
.
Так как 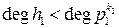 ,
, 
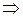
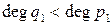 . Рассуждая подобным образом, получаем, что для любого
. Рассуждая подобным образом, получаем, что для любого 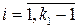 справедливы неравенства
справедливы неравенства 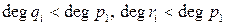 .
.
Так как
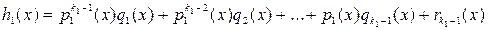 ,
,
то
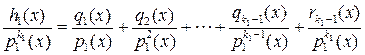 . (1.6.5)
. (1.6.5)
Таким образом, доказали, что произвольная правильная рациональная дробь разлагается в сумму простейших дробей.
Для доказательства однозначности разложения в сумму простейших дробей рассмотрим соотношение (1.6.5). Допустим, что существует другое разложение дроби
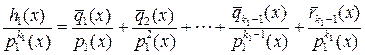 .
.
Вычитая данное соотношение из (1.6.5), имеем
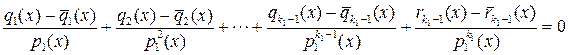 .
.
Умножая обе части на полином 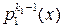 , получаем, что сумма полинома и правильной дроби равна нулю, что, однако, невозможно.
, получаем, что сумма полинома и правильной дроби равна нулю, что, однако, невозможно.
 2014-02-09
2014-02-09 690
690








