Свойства плотности.
1. 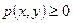 (функция распределения – неубывающая функция).
(функция распределения – неубывающая функция).
2. 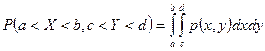 (по свойству 5 функции распределения) Справедливо обобщение
(по свойству 5 функции распределения) Справедливо обобщение 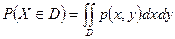 .
.
3. 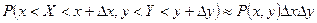
4. 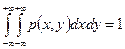 (по свойству 4 функции распределения)
(по свойству 4 функции распределения)
5. 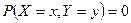
6. 
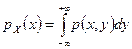 ,
, 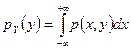 (Свойство 7 функции распределения)
(Свойство 7 функции распределения)
Случайные величины X, Y называются независимыми, если 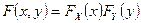 , где
, где 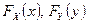 - функции распределения случайных величин X, Y.
- функции распределения случайных величин X, Y.
Если случайные величины непрерывны, то, дифференцируя это соотношение по x, y, получим 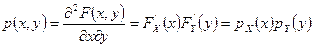 .
.
Соотношение 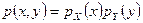 поэтому можно считать определением независимости непрерывных случайных величин.
поэтому можно считать определением независимости непрерывных случайных величин.
Для дискретных случайных величин определение независимости можнозаписать в виде 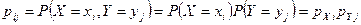 .
.
 2014-02-12
2014-02-12 334
334








