Пусть число испытаний n велико, вероятность p мала и 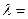 np мало. Тогда вероятность наступления m успехов в n испытаниях можно приближенно определить по формуле Пуассона:
np мало. Тогда вероятность наступления m успехов в n испытаниях можно приближенно определить по формуле Пуассона: 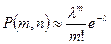 .
.
Заметим, что по формуле Пуассона можно считать вероятность неуспеха, если q мало, приняв 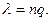
Случайная величина с рядом распределения m, 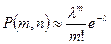 имеет распределение Пуассона. Чем больше n, тем формула Пуассона точнее. Для грубых расчетов формулу применяют при n =10,
имеет распределение Пуассона. Чем больше n, тем формула Пуассона точнее. Для грубых расчетов формулу применяют при n =10, 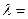 0 – 2, при n = 100
0 – 2, при n = 100 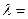 0 – 3. При инженерных расчетах формулу применяют при n = 20,
0 – 3. При инженерных расчетах формулу применяют при n = 20, 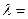 0 – 3, n =100,
0 – 3, n =100, 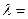 0 – 7. При точных расчетах формулу применяют при n = 100,
0 – 7. При точных расчетах формулу применяют при n = 100, 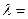 0 – 7, n =1000,
0 – 7, n =1000, 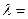 0 – 15.
0 – 15.
Вычислим математическое ожидание и дисперсию случайной величины, имеющей распределение Пуассона.
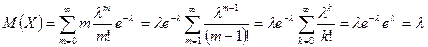 ,
,
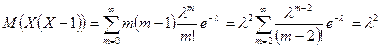
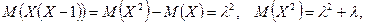
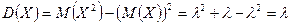
 2014-02-12
2014-02-12 577
577








