Другие распределения, часто используемые в инженерных расчетах

Распределение Вейбулла. Это распределение с плотностью

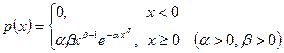
и функцией распределения

.

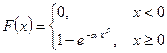Если 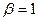, то распределение Вейбулла превращается в экспоненциальное, а при 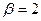- в распределение Релея.

Достаточно близкую к распределению Вейбулла плотность имеет гамма – распределение:

.

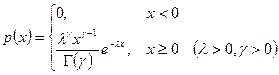Здесь 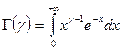- гамма-функция.

Если 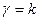- целое число, то гамма-распределение превращается в распределение Эрланга порядка k. Если k – нечетное число, 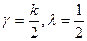, то гамма-распределение превращается в распределение 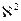(хи-квадрат) распределение с k степенями свободы.

При 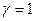(так как 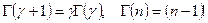) гамма-распределение переходит в экспоненциальное.

Для всех рассмотренных распределений составлены таблицы, по которым можно определять значения функций распределения.