Пример № 2.2

Рассмотрим ламинарное установившееся стационарное неизотермическое течение ньютоновской жидкости через длинную трубку круглого сечения радиуса R. Температура стенки трубы T_w поддерживается постоянной. Задача состоит в отыскании распределения скорости и температуры в поперечном сечении трубы, удалённом от входа.

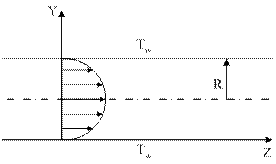
В этой задаче все производные температуры, скорости, напряжения по переменным z, q, t равны нулю.

Уравнения движения и энергии:

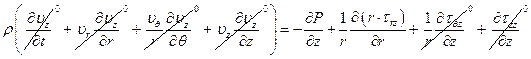
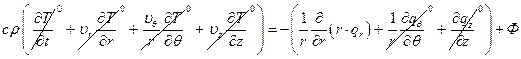
Останется:

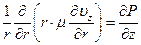(2.10)

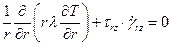(2.11)

Перепишем уравнение энергии, вводя в него выражения для t_rz и :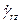

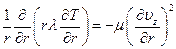
Граничные условия задачи:

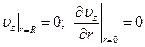(2.12)

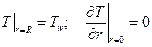(2.13)

Интегрируем уравнение (2.10):

,

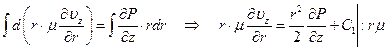
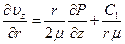Из ГУ (2.12) С₁=0, получим:

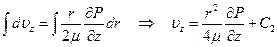
Найдем С₂:

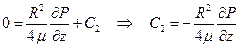
Тогда скорость будет равна:

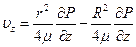или

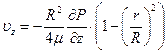
Знак “-” показывает на то, что жидкость течёт в направлении уменьшения давления. Подставляя полученное выражение для u_z в уравнение энергии, можем найти температуру.

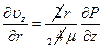
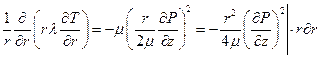
Интегрируя, заменив для удобства константу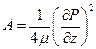

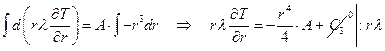
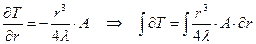
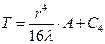
Найдем С₄:

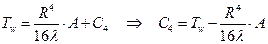
Окончательное выражение для температуры:

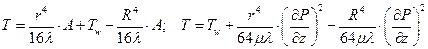или

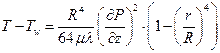
Скорость и температура жидкости на оси рассчитывается по тем же формулам.