Допущение о постоянстве теплофизических характеристик

При решении ряда задач о течении и теплообмене полимерных материалов часто используют предположение о постоянстве l, C, r (считаются независимыми от P и t⁰). При наложении полиэтиленовой изоляции типичное изменение температуры составляет 100⁰С, а давление изменяется на 500Мпа. При этих условиях плотность типичного полимера будет изменяться на 10-20% в зависимости от того кристаллический он или аморфный, в то время как вариации, и C_р, более значительны и составляют 30-40%.

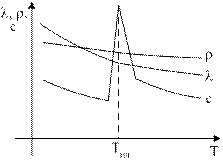
Гипотеза о постоянстве l, C, r может повлиять на результаты расчётов. Если это влияние существенно, то прибегают к ряду математических методов, позволяющих учитывать изменение зависимость этих характеристик от температуры. Таким образом, для каждой конкретной задачи течения и теплообмена записываются определяющие уравнения, условия однозначности, делаются допущения.

Пример № 2.1. Рассмотрим течение ньютоновской жидкости, ламинарное, стационарное*6, установившееся*7, неизотермическое, между двумя бесконечными параллельными пластинами.

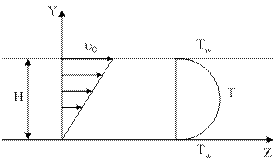
Пластины находятся на расстоянии H друг от друга, которое много меньше по сравнению с длиной и шириной пластин. Нижняя пластина неподвижна, а верхняя движется с постоянной скоростью u₀ в направлении Z. Температура обеих пластин T_w поддерживается постоянной. Предполагается, что все свойства жидкости, включая плотность и вязкость, неизменны.

Искомые величины в этой задаче T, u, t являются функцией только одной независимой переменной – пространственной координаты Y. Следовательно, все производные этих величин (T, u, t) относительно x, z, t равны нулю. Кроме того, только u₀ является ненулевой компонентой скорости и q_v¹0.

Для этого частного случая уравнения движения и энергии в прямоугольных координатах примут вид:

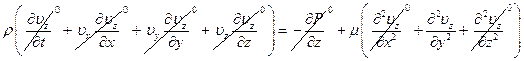остается:

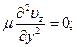(2.5)

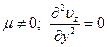, значит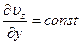

Аналогично для уравнения энергии:

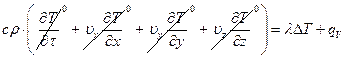останется:

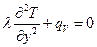(2.6)

Постановка задачи – совокупность определяющих уравнений, граничных и начальных условий. Количество ГУ и н.у. определяется порядком производных, входящих в систему уравнений.

Граничные условия этой задачи имеют вид:

по скорости: 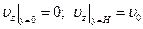(2.7)

по температуре: 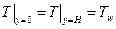(2.8)

Задача задана (поставлена) уравнениями (2.5¸2.8).

Интегрируем уравнение (2.5):

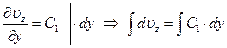получим выражение для скорости: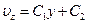

Определим константы C₁ и C₂(подставив граничные условия в выражение для скорости):

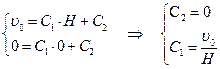
Тогда выражение для скорости запишется:

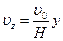
Производная скорости:

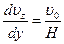
Рассмотрим уравнение (20), функция диссипации определяются следующим образом:

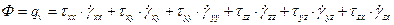
В результате уравнение энергии:

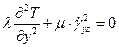
Распишем 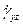(реологический закон):

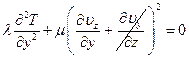
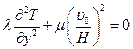, интегрируем:

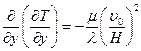, (2.9)

Обозначим правую часть уравнения (2.9) за B, это константа.

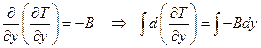
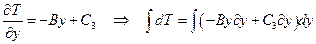
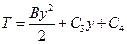
Определим константы C₃ и С₄:

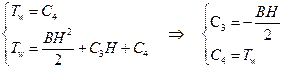
Тогда окончательный вид для температуры:

Скорость – линейная функция координаты. Распределение T по зазору является параболическим. В целом нужно отметить, что задача в данной постановке является не связанной, т.к. можем прийти к решению отдельно каждого уравнения (2.5, 2.6). В случае , задача являлась бы связанной.