При проведении экспериментов на капиллярном вискозиметре особое внимание уделяют обеспечению однородного поля температур и исключением потерь на трение с поршнем и цилиндром.
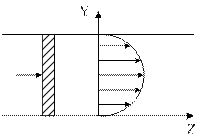 | Рассмотрим капилляр. Мы не учитываем массовые силы, поэтому не важно, как расположен капилляр, вертикально или горизонтально. В качестве исходной точки для определения количественной оценки зависимости 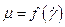 используют уравнение движения (в цилиндрической СК). используют уравнение движения (в цилиндрической СК). |
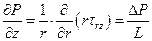 , где (3.6)
, где (3.6)
L - длина капилляра, DP – перепад давления;
Интегрируем уравнение (3.6), заменим для простоты trz на t, получим:
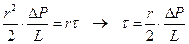 (3.7)
(3.7)
Это зависимость от радиуса и перепада давления, мы же стремимся получить зависимость t от 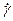 , а по этой закономерности можно построить зависимость
, а по этой закономерности можно построить зависимость 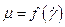
Напряжение сдвига на стенке r=R:
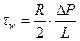 (3.8)
(3.8)
Реологический закон выполняется для любой точки среды, следовательно и на приемлемом участке:
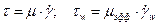
Из последнего уравнения следует, что, если из эксперимента удаётся определить величину 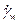 , то можно установить зависимость вязкости от напряжения сдвига или от скорости сдвига.
, то можно установить зависимость вязкости от напряжения сдвига или от скорости сдвига.
Это можно сделать, измеряя величину объемного расхода Q:
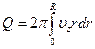 , возьмем по частям*8:
, возьмем по частям*8:
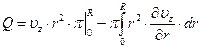 (3.9)
(3.9)
Первое слагаемое выражения (3.9) равно нулю, так как при r=R из условия прилипания к стенкам uz=0, получим:
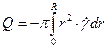 (3.10)
(3.10)
Из выражения (3.7) определим, чему равен r и dr:
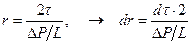 (3.11)
(3.11)
Подставив (3.11) в (3.10), получим:
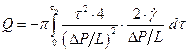 (3.12)
(3.12)
Из (3.8) выразим 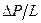 :
:
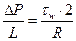 (3.13)
(3.13)
После подстановки уравнения (3.13) в (3.12), получим:
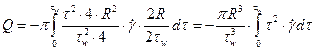
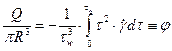 ,
,
Возьмем производную 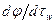 :
:
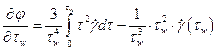 *9 (3.14)
*9 (3.14)
Умножим (3.14) на tw, преобразуем, получим:
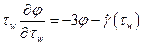
Выразим 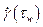 :
:
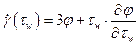 (3.15)
(3.15)
В выражение (3.15) вместо j подставим выражение через расход, вместо tw – выражение (3.8), т.е. 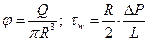 , получим:
, получим:
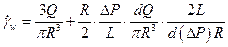
Окончательно имеем:
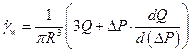
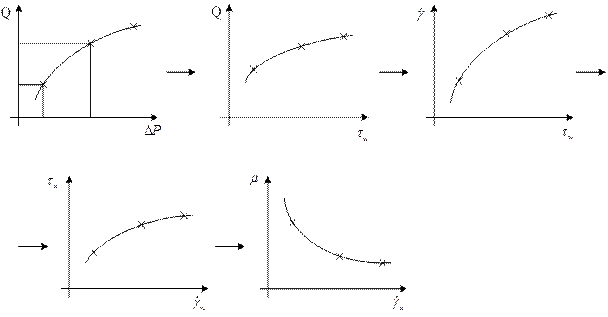
Теперь имея экспериментальную кривую 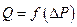 определяем при каждом значении DP значение
определяем при каждом значении DP значение 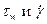 ® можно построить зависимость
® можно построить зависимость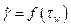 ,
, 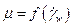
 2014-02-12
2014-02-12 838
838








