Пересечение прямой линии с многогранными и кривыми поверхностями

Прямая может пересекать поверхность многогранника в двух и более точках. Если многогранник выпуклый, то прямая пересечет его в двух точках. Выпуклым называют многогранник, если он весь лежит по одну сторону любой его грани. Рассматриваемая задача сводится к построению точек пересечения прямой с плоскостями, так как многогранная поверхность представляет собой совокупность плоскостей.

На рис. 46 приведен пример построения на комплексном чертеже точек пересечения E и F прямой l с треугольной пирамидой SABC.

Решение задачи проводим по следующему алгоритму:

1) через заданную прямую проводим вспомогательную фронтально проецирующую плоскость - Φ É l, Φ ^ П₂;

2) строим линию пересечения посредника с поверхностью пирамиды - Φ ∩ SABC = 123;

3) находим точки пересечения построенной линии с заданной прямой - E = 12 ∩ l и F = 23 ∩ l.

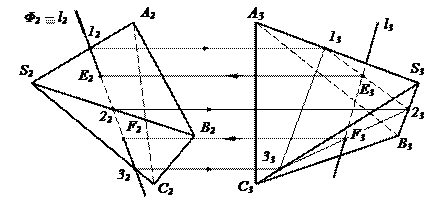Рис. 46

Пересечение прямой с кривыми поверхностями рассмотрим на примерах пересечения с поверхностями второго порядка – цилиндрической, конической и сферической. Точек пересечения, исходя из порядка поверхности, две. В качестве посредника для их определения выбираем плоскость, проходящую через прямую и пересекающую заданную поверхность по простейшим линиям. Для цилиндрической поверхности такой плоскостью должна быть плоскость, параллельная образующим, для конической плоскость, проходящая через вершину поверхности, а сферической любая плоскость. В первых двух случаях вспомогательная плоскость пересечет поверхности по прямым линиям, а в случае со сферой по окружности.

На рис. 47, а и б приведены наглядные чертежи, на которых показано построение точек пересечения прямой с цилиндрической и конической поверхностями.

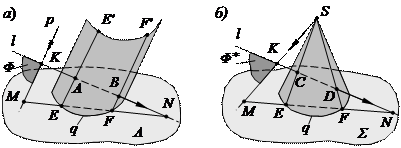
Рис. 47

Рассмотрим алгоритм нахождения этих точек:

1) вспомогательные плоскости Φ (p ∩ l) и Φ* (SK ∩ l) проводим через заданную прямую l соответственно параллельно образующим цилиндрической поверхности и вершину S конической поверхности;

2) строим прямые пересечения EE, EE' и SE, SF вспомогательных плоскостей Φ и Φ* с конической и цилиндрической поверхностями, для чего предварительно находим прямые MN, которые являются результатом пересечения посредников Φ и Φ* с плоскостями оснований Λ и Σ заданных поверхностей. Точки E и F получаем в пересечении прямых MN с линиями оснований q;

3) определяем точки пересечения построенных прямых с заданными, т. е. A = EE' ∩ l, B = FF' ∩ l, C = SE ∩ l, D = SF ∩ l.

На рис. 48 приведен пример построения на комплексном чертеже точек пересечения прямой профильного уровня со сферической поверхностью. В качестве посредника используем плоскостью (Φ) профильного уровня, так как линия ее пересечения со сферической поверхностью - окружность - изображается на профильную плоскость проекций в натуральную величину. Дальнейшие построения проводим в соответствии с алгоритмом и как результат получаем искомые точки А и В.