2014-02-12
1784
а) В пути все вершины, кроме терминальных, имеют степень 2, а терминальные – 1.
б) Любая вершина цикла имеет степень 2 или другую четную степень.
в) Число вершин в пути на единицу больше, чем ребер, а в простом цикле число ребер равно числу вершин.
| v 1 | v 2 | v 3 | v 4 | ||
| v 1 | |||||
| S= | v 2 | ||||
| v 3 | |||||
| v 4 |
г) Если S – матрица смежности графа G, то (i, j)‑ый элемент матрицы Sk равен числу (vi ‑ vj)маршрутов длины k.
Пример: по заданной матрице смежности определить число маршрутов длины 3 между любой парой вершин в графе.
Вычислим последовательно степени матрицы S.
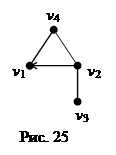
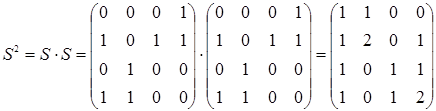
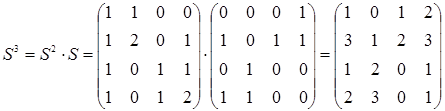
Из полученной матрицы S 3 следует, что имеется один (v 1‑ v 1)-маршрут длины 3, три (v 2‑ v 1)-маршрута длины 3, один (v 3‑ v 1)-маршрут длины 3, два (v 4‑ v 1)-маршрута длины 3 и т.д.. Все маршруты легко восстанавливаются по матрицам S 3, S 2 и S. Восстановим, например, (v 3‑ v 1)-маршрут: элемент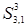 
, равный единице, был получен в результате умножения элементов 
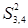и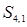 
, в свою очередь элемент 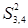получился путем умножения 
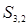и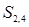 
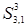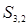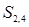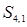. Тем самым, в формировании элемента участвовали элементы , и матрицы смежности, поэтому (v 3‑ v 1)-маршрут есть последовательность вершин (3,2,4,1). Наглядным подтверждением полученного решения является рисунок 25.
