Циклический и коциклический ранг графа

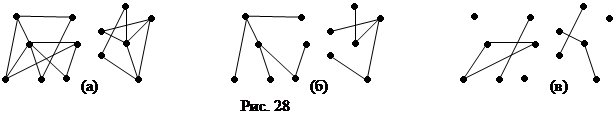
Цикломатическим числом или циклическим рангом графа называется наименьшее число ребер, которое необходимо удалить из графа так, чтобы в нем не осталось ни одного цикла. После такого удаления ребер из связного графа будет получено дерево, называемое остовным деревом или остовом графа (в случае несвязного графа – остовный лес). Заметим, что число вершин в остове совпадает с числом вершин графа. Относительное дополнение остова до исходного графа образует так называемое ко-дерево (ко-лес) для данного остова. Ребра остова называют ветвями, а ребра ко-дерева (ко-леса) – хордами.

На рисунке 28 (а) изображен несвязный граф, а на рисунках (б) и (в) его остовный лес и соответствующий ему ко-лес.

Обозначим цикломатическое число графа g(G), число ребер р, число вершин в и число компонент k. Тогда из определения цикломатического числа следует, что р ‑ g(G) = в –1 для связного графа и р ‑ g(G) = в – k для несвязного графа. Отсюда g(G) = р ‑ в+ 1 для связного и g(G) = р ‑ в+k для несвязного графов соответственно. Цикломатическое число характеризует связность графа или, как говорят, является мерой связности. Заметим также, что число хорд в ко-лесе равно g(G).

Нетрудно установить, что цикломатическое число дерева равно нулю, а простого цикла – единице.

Число ветвей в остове (в – k) называют коциклическим рангом графа или рангом разреза и обозначают g*(G). Заметим, что g(G) +g*(G)= р.

Разделяющим множеством простого графа называют такое подмножество его ребер, удаление которого увеличивает число компонент графа.

Разрезом (коциклом) в графе называется такое разделяющее множество, никакое собственное подмножество которого не является разделяющим. Таким образом, удаление разреза из графа увеличивает число его компонент в точности на единицу. Если разрез состоит из единственного ребра, то он называется перешейком или мостом.

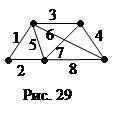Для графа на рисунке 29 множества ребер {1,2,5} и {3,4,6,7,8} являются разделяющими множествами. А множества {1,2} и {3,6,7,8} – разрезами.

Следующая теорема устанавливает связь между остовами и разрезами, а также между ко-лесом и циклами в графе.

Теорема 3.10.1. Пусть Т – остовный лес графа G, а K – соответствующий ему ко-лес. Тогда (а) всякий разрез в G имеет общее ребро с Т, и (б) каждый цикл в G имеет общее ребро с K.

Доказательство: (а) Пусть С – разрез графа G, удаление которого разбивает одну из компонент графа на два подграфа Н и Р. Поскольку Т – остовный лес, то в нем обязательно содержится ребро, соединяющее некоторую вершину из Н с некоторой вершиной из Р. Это и есть ребро разреза С.

(б) Пусть теперь С – цикл в G, не имеющий общих ребер с К. Тогда из определения ко-леса К следует, что все его ребра С должны содержаться в Т, а это невозможно, т.к. в Т нет циклов.

Связь между циклами и разрезами устанавливается следующей теоремой.

Теорема 3.10.2. Любой цикл и любой разрез связного графа имеют четное число общих ребер.

Доказательство: пусть С – цикл и S – разрез в графе G. Удаление ребер S из G разбивает его на два связных подграфа Н и Р. Если цикл С содержится полностью в одном из этих подграфов, то число общих ребер С и S равно нулю, что не противоречит четности. Если же С не содержится целиком ни в Н, и ни в Р, то число общих ребер должно быть больше нуля. Будем передвигаться по циклу, начиная из вершины v ₁Î Н. Тогда, перемещаясь в Р, мы должны будем пройти через ребро, принадлежащее S, но т.к. движение по циклу должно закончиться в v ₁, то существует обратное ребро из Р в Н, также принадлежащее S. А это возможно только в том случае, когда С и S имеют четное число общих ребер.