Энтропия объединений. Условная энтропия

Объединением называются совместные опыты со взаимозависимыми исходами. Пример объединения – действие источника и приёмника сигналов в канале с помехами, если заданы вероятностные характеристики источника, приёмника и процесса передачи сигналов.

Источник производит сигнал х₁, х₂, … х_i,… х_m, приёмник принимает y₁, y₂, … y_i,… y_m при этом заданы распределения безусловных вероятностей p(х₁), p(х₂), … p(х_i),… p(х_m), а также условных вероятностей y_j /x_i, x_i /y_j .

Как известно, безусловные и условные вероятности в совместных опытах связаны выражением

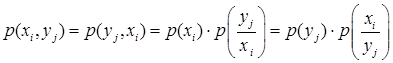(1.45)

На основе этого энтропия объединения

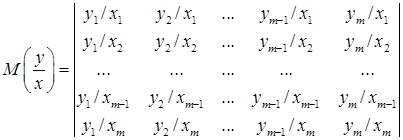(1.46)

Действие помех приводит к тому, что передавая сигнал х_i, в последовательности будет получать разные сигналы y_j, что и отражается канальной матрицей.

Задавая качественные признаки сигналов (частоту, фазу и др.) в соответствии с характеристиками помех обеспечивают наибольшие значения условных вероятностей на главной диагонали матрицы, что и обеспечивает возможность передачи информации по каналу.

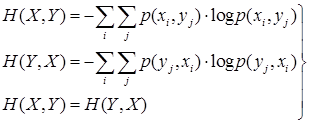(1.47)

С учётом (1.45) получим

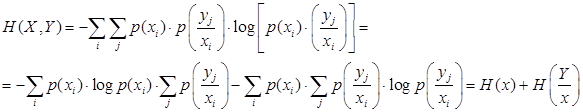(1.48)

В преобразованиях (1.48) использованы замены двойных сумм вложенными, также тот факт, что сумма условных вероятностей

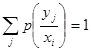(1.49)

В выражении (1.48) первое слагаемое – это энтропия источника Н(X) , а Н(Y/X) – это средняя условная энтропия – мера неопределённости того, какой ансамбль принятых сигналов соответствует ансамблю переданных. Эта энтропия складывается из частных условных энтропий

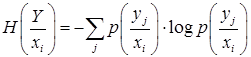(1.50)

путём их усреднения с учётом распределения безусловных вероятностей p(x_i)

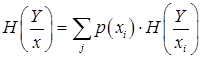(1.51)

Частная условная энтропия – мера неопределённости принятого ансамбля относительно переданного сигнала x_i

На основании двойственности зависимости (1.45) можно записать

H(Y,X) = H(Y) + H(X/Y) (1.52)

Условные вероятности p(y_j/x_i) могут принимать граничные значения p(y_j/x_i) = 1, если принятые сигналы такие же, как и переданные и p(y_j/x_i) = p(y_j), т.е. какая-либо связь между переданными и принятыми сигналами отсутствует.

В первом случае

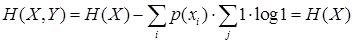(1.53)

или H(Y,X) = H(Y)H(X) = H(Y)

Во втором

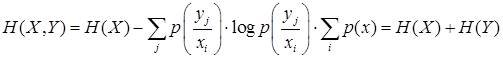
т.к. 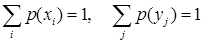(1.54)

Из (1.54) следует, что энтропия объединения здесь достигает максимума, а передача информации от источника к приёмнику отсутствует.