Анализ свойств эргодических последовательностей (Э.П.) позволяет установить следующее:
- если длины последовательностей элементов, выработанные эргодическими исчислениями превышают некоторое значение n>n0, то эти последовательности распадаются на 2 класса:
1. Нетипичные, сумма вероятностей которых меньше сколь угодно малой величины при n→∞.
2. Типичные, которые только и вырабатывает практически и вырабатывает эргодические источники. Такое разделение последовательностей х связано с неравновероятностью и взаимозависимостью появления элементов Э.П.; если элементы последовательности равновероятны и взаимонезависимы, то разделения её на классы типичных и нетипичных исчезает.
Таким образом, совокупность типичных последовательностей позволяет судить о существовенных вероятностных характеристиках Э.П.
Покажем это следующим образом. Число нахождения эргодического источника в состоянии Sk на интервале последовательности длиной n.
Nk = n p (Sk) (1.35
)
Число переходов из состояния Sk в состояние Se здесь
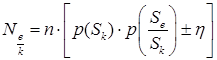 (1.36)
(1.36)
Введением вероятности η учитываем тот факт, что в Э.П. конечной длины может отсутствовать часть состояний и переходов.
Вероятность того, что на интервале n произойдёт Ne/k переходов
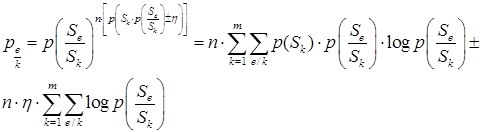 (1.37)
(1.37)
или 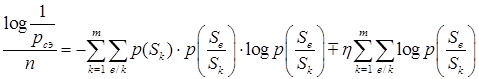 (1.38)
(1.38)
Первое слагаемое в последнем уравнении – это энтропия эргодического источника, Н (x). Второе слагаемое
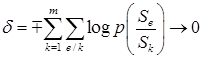 при n→∞. (1.39)
при n→∞. (1.39)
Таким образом
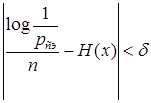 (1.40)
(1.40)
Первое слагаемое в (1.38) представляет собой энтропию конкретной Э.П. длиной n. С увеличением n
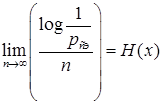 (1.41)
(1.41)
Последние два уравнения и являются основой исходных утверждений о типичных и нетипичных последовательностях.
При достаточно больших n δ →0 и (1.40) преобразуем следующим образом
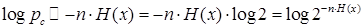 или
или 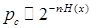 (1.42)
(1.42)
По определению рассматриваемые последовательности будут типичными и приблизительно равновероятными, а их число будет
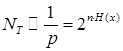 (1.43)
(1.43)
Если мощность алфавита источника m, то число всевозможных последовательностей длины n составляет N=mn.
Отсюда получим
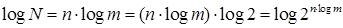 и N = 2 n∙log m (1.44)
и N = 2 n∙log m (1.44)
Число разновидностей типичных последовательностей составляет малую часть N, хотя они в основном и производятся эргодическим источником.
Покажем это на следующем примере. Пусть двоичный источник производит элементы 0 и 1 с равными вероятностями p (0) = p (1), а вероятностные связи между элементами последовательности снижают энтропию источника до H (x) = 0,9 бит/эл, по отношению к Нmax = log m = log 2 = 1 бит/эл.
Все возможные двоичные комбинации n
000…000 – все нули
000…001 – одна 1, остальные 0
000…010 – одна 1, остальные 0
000…011 – две 1, остальные 0
..
100…000 - одна 1, остальные 0
..
111…111 – все 1
при p (0) = p (1) к типичным будут относиться последовательности, у которых число 0 и 1 мало будет отличаться друг от друга.
Если взять n =50, то
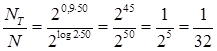 ,
,
А уже при n = 100 доля типичных последовательностей снижается
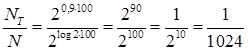
 2014-02-12
2014-02-12 2682
2682








