477
Задача 6.2
В условиях задачи 6.1 определить числовые характеристики случайной величины Х – количества домов, которые сданы в эксплуатацию в запланированный срок. Найти также моду μ и вероятность попадания случайной величины Х в интервал значений [0; 2,5).
Решение. Найденный раньше ряд распределения случайной величины Х имеет вид
| xi | ||||
| pi | 0,001 | 0,027 | 0,243 | 0,729 |
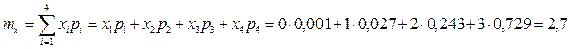Математическое исповедание mx случайной величины Х определяют по формуле (6.1) при n = 4:
Дисперсию случайной величины Х определяют за формулой (6.10):
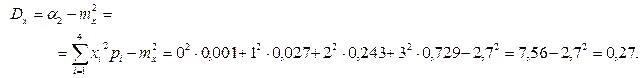
Среднее квадратичное отклонение случайной величины Х определяют по формуле (6.13):
.
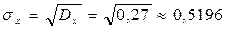Найдем моду μ. μ = 3 поскольку значению x4= 3 отвечает максимальная вероятность p3 = 0,729.
Вероятность попадания случайной величины в заданный интервал значений от х1 = 0 до х2 = 2,5 можно определить двумя способами:
а)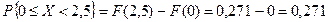 
.
б)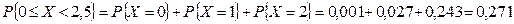 
.
Задача 4.3.Непрерывная случайная величина Х задана плотностью распределения
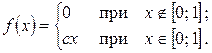
Найти значение плотностью постоянной с, интегральную функцию распределения F(х). Построить график плотности распределения f(х), графики интегральной функции распределения F(х). Определить математическое ожидание mx дисперсию Dx , середнєквадратичне отклонение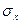
, медиану Me и вероятность попадания случайной величины в интервал (0; 0,5).
Решение. Постоянная величина с определяется с помощью свойства плотности распределения (5.3)
.
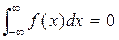Поскольку задана f(х)– кусочно-непрерывная, то рассматривается сумма интегралов на промежутках непрерывности:
.
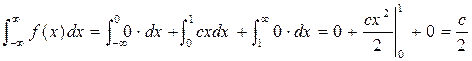Получаем уравнение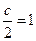 
, из какого с = 2.
Плотность распределения приобретет вид: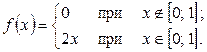 
Интегральную функцию распределения определяют по формуле (5.6) для каждого промежутка непрерывности:
при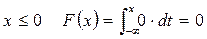 
;
при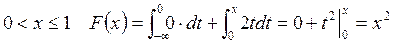 
;
при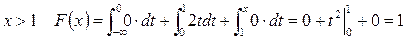 
.
Окончательно получаем: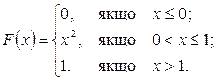 
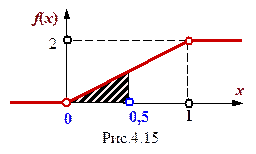
Графики f(х)и F(X) имеют вид
| |
| |
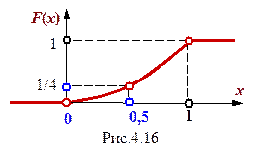
Математическое ожидание mx определяют по формуле (6.1):
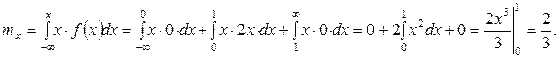
Дисперсию Dx определяют по формуле (6.10):
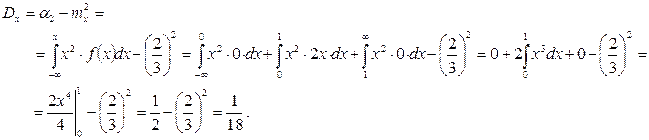
Среднее квадратичное отклонение найдем по формуле (6.13):
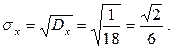
По определению медианы Р{X<Me}= P{X>Me}. Следовательно, медиану можно найти по уравнению (6.12)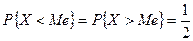 
.
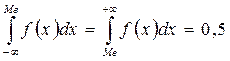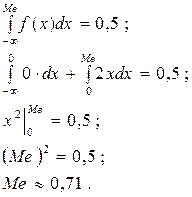
Искомую величину P{0<X< 0,5} определим двумя способами:
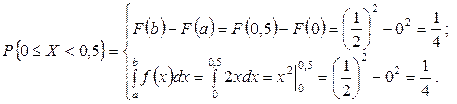
Найденной вероятности отвечает заштрихованная площадь на графике плотности вероятности.
