Определяется видимость ГО

Определяются точки пересечения заданного ГО и построенной линии пересечения

Строится недостающая проекция этой линии пересечения

Строится линия пересечения заданного ГО со вспомогательной плоскостью

Заданная линия заключается во вспомогательную плоскость-посредник

Алгоритм решения задач

Задача 4:Построить точку пересечения прямой линии MN и плоскости ΔАВС

Дано Решение

n1

n2

m1

m2

С1

С2

В1

В2

А1

А2

K2

K1

21

22

11

12

n1

n2

m1

С1

С2

В1

В2

А1

А2

Решение:

Σ2

1. Через линию m₂n₂ провести вспомогательную фронтально-проецирующую плоскость

2. Плоскость Σ₂ пересекает фронтальную проекцию ΔАВС по прямой 1₂2₂

3. Строится горизонтальная проекция прямой 1₁2₁

4. m₁n₁ пересекается с 1₁2₁ в точке К₁

5. Строится фронтальная проекция К₂

6. Определяется видимость геометрических образов

Определение высоты точек

На П₁ выше та точка, фронтальная проекция которой дальше от оси Х

На П₂ выше та точка, горизонтальная проекция которой дальше от оси Х

Задача 5: Построить линию пересечения плоскостей ΔАВС и ΔDEF

E2

Дано:

В2

E1

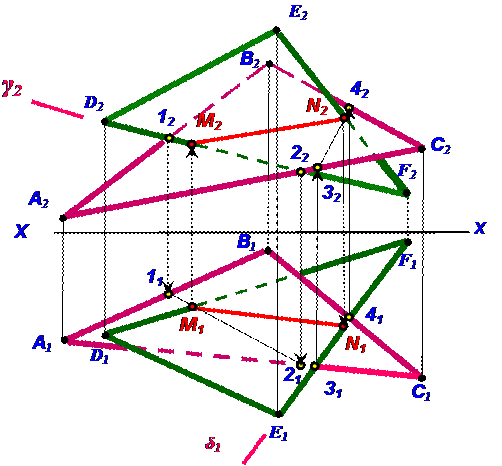
Решение:

Решение:

1. Линия D₂F₂ заключается в вспомогательную плоскость-посредник γ₂,

γ₂ перпендикулярна П₂

2. γ₂ ∩ β₂ = 1₂2₂

3. 1₁2₁

4. 1₁2₁∩D₁F₁= М₂

5. М₁

6. Линия Е₁F₁ заключается в вспомогательную плоскость-посредник δ₁,

δ₁ перпендикулярна П₁

7. δ₁∩ β₁= 3₁4₁

8. 3₂4₂

9. 3₂4₂ ∩ Е₂F₂ = N₂

10. N₁

11. М₂N₂, М₁N₁

12 Определить видимость линий на чертеже

Задача 6: Построить точки пересечения наклонной пирамиды с прямой общего положения

Дано Решение

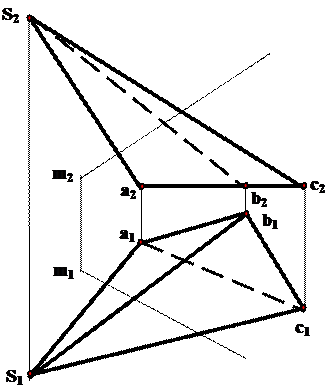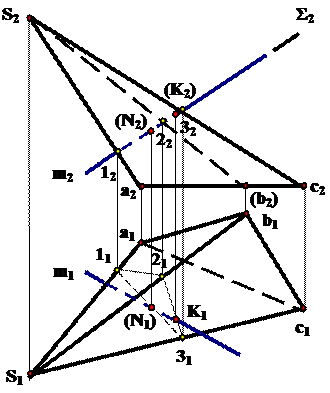
Решение:

1. Через m₂ провести вспомогательную плоскость-посредник Σ₂, перпендикулярную фронтальной плоскости проекций.

2. Σ₂ пересекает фронтальную проекцию пирамиды по треугольнику 1₂2₂3₂

3. Построить горизонтальную проекцию этого треугольника 1₁2₁3₁

4. Отметить точки пересечения треугольника 1₁2₁3₁ с m₁ – N_1, К₁; N_2, К₂

5. Определить видимость прямой m

Пересечение поверхностей

В зависимости от расположения и формы поверхностей задачи делятся на группы:

1. Одна поверхность – проецирующая (задача 2).

2. Обе поверхности имеют общую ось симметрии и их оси параллельны

(метод секущих плоскостей - задача 7).

3. Обе поверхности – это поверхности вращения и их оси пересекаются

(метод секущих сфер – задача 8).

Метод секущих плоскостей

Задача 7: Построить линию пересечения конуса и сферы

Дано Решение

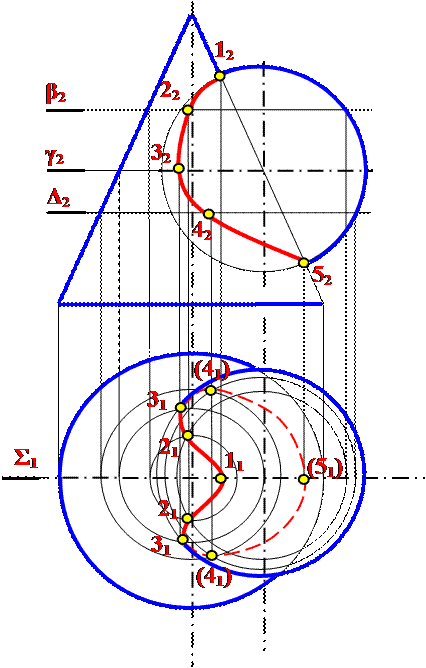Метод секущих сфер

Задача 8: Построить линию пересечения конуса и наклонного цилиндра

Дано Решение

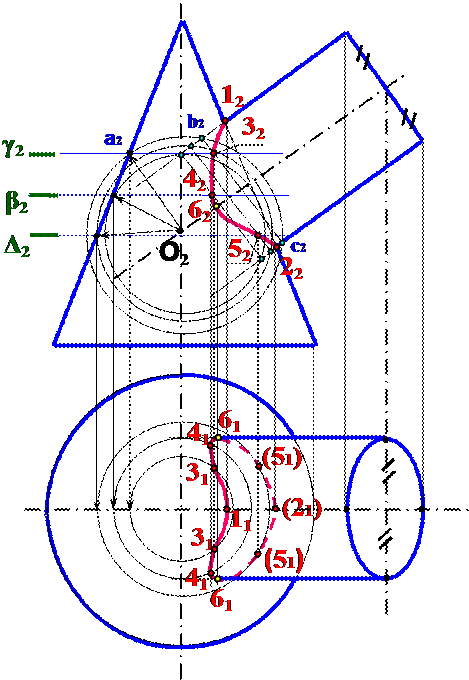
Ход решения:

1. Опорные точки 1₂, 2₂;

2. 1₁, 2₁;

3. γ₂ – перпендикулярно П₂;

4. а₂;

5. Провести окружность из центра в О₂ радиусом О₂ а₂;

6. Окружность пересекает боковые образующие цилиндра в точках b₂, c₂;

7. b₂ c₂ ∩γ₂ = 3₂;

8. 3₁;

9. Аналогично строятся точки 4,5;

10. Точка 6₂ лежит на пересечении линии 1₂ 3₂ 4₂ 5₂ 2₂ с осевой линией цилиндра;

11. 6₁;

12. соединить плавной линией полученные точки.