Дихотомическая процедура. Использование процедуры деления понятия в процессе принятия решений

Ключевые понятия темы: Логическая структура суждения. Состав суждения. Виды суждений. Отношения между суждениями.

В простом атрибутивном суждении имеются: субъект, предикат, связка, квантор.

Пример. Всестудентыявляютсяучащимися высшего учебного заведения.

Субъект это студенты (-)

Предикат – учащимися высшего учебного заведения (=)

Квантор – все (~)

Связка – является (--)

Предикат – это имя свойства или отношения между объектами с последовательностью аргументов.

Субъектом атрибутивного суждения называют понятия о предмете суждения и обозначают (S).

Предикатом атрибутивного суждения называют понятие о признаке предмета, рассматриваемого в суждении (P).

Связка может быть выражена словом (есть, суть, является) или группой слов, тире, или простым согласованием слов. Перед объектом суждения иногда стоит кванторное слово. Квантор всеобщности (общности): ". Квантор существования: $. Кванторное слово указывает, относится ли суждение ко всему классу понятия, или к его части.

Виды простых суждений:

1) Суждение свойства или атрибутивные суждения. Суждение этого вида утверждается или отрицается принадлежащих предмету известных свойств, состояний, видов деятельности.

2) Суждения отношения. В этих суждениях отображается отношение минимум двух объектов по величине, последовательности, качеству, положению, времени, связи, причине и следствию, родству и т.д.

Формула выражения суждения с двухместным отношением записывается как aHb, H (a,b), где a и b имена предмета, H – имя отношения. В данном суждении может, что - либо отрицаться или утверждаться не о двух, а о трёх, четырёх и нескольких предметов H (a1, a2,..., an)

3) Суждения существования (экзистенциальные) в них утверждается или отрицается существование предметов в материальной или идеальной действительности.

Традиционная логика разделяет все категорические суждения на два вида. По качеству связки (есть), категорические делятся на утвердительные и отрицательные. В зависимости от того обо всём классе предметов, или о части этого класса, или об одном предмете идет речь в субъекте, суждения делятся на общие ((квантор всеобщности ")S есть P), частные (некоторые $ S есть P) и единичные (S есть P).

Объединенная классификация простых категорических суждений по количеству и качеству могут быть распределены, либо не распределены. Термин считается распределенным, если его объём полностью включается в объём другого термина или наоборот исключается из него. Термин будет не распределенным, если его объем частично включается в объем другого термина или частично исключается. Рассмотрим на примерах:

1. Общеутвердительные суждения (А)

P –
S -

Пример. Все эффективные менеджеры играют важную роль в работе фирмы.

2. Частноутвердительное (I)

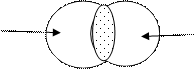S P

1) Некоторые студенты – спортсмены

2) Некоторые студенты отличники

S - P -

3. Общеотрицательные (E)
S

P

Ни один лев не является травоядным животным

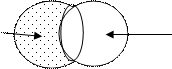4. Частноотрицательные (О)]

S P

Некоторые менеджеры не являются руководителями фирмы

Тема 4: Алгебра логики высказываний

Ключевые понятия темы: Логические связки, правила истинности логических связок. Алгоритм построения таблицы истинности. Нормальные формы. Тождественные формулы. Логические следствия. Значение в менеджменте.

Сложное высказывание образуется из простых двумя способами:

1) путём квантификации высказываний;

2) объединением простых элементарных с помощью логических связок.

Первый способ представляет собой метод получения общих суждений путем использования логических кванторов характеризующих объем суждения.

Рассмотрим понятия функции высказываний. Функция высказываний оценивается с точки зрения их истинного значения, поэтому такая функция называется истинной. Она образуется по аналогии математической функции. Но аргументами в ней являются не числа, а логические объекты – высказывания, которые приобретают значения 0 или 1. Поэтому данную функцию ещё называют пропозициональной.

Таким образом, один из способов образования высказывания состоит в том, что сначала мы составляем пропозициональную функцию, где фигурирует соответствующие переменные, а затем связываем их кванторами всеобщности и существования.

Второй способ состоит в объединении двух или более простых высказываний с помощью логических связок. Их всего пять.

Основные логические связки:

1) Отрицание, буквально означает противоположное тому, что утверждалось, читается, как (не) А, обозначается как «ùА». Характер носит отрицающий.

2) Конъюнкция (логическое умножение), обозначается знаком «^». В речи и на письме носит характер союза «и». Характер носит соединительный.

3) Дизъюнкция (логическое сложение), встречается двух видов строгая или не строгая. В речи и на письме носит характер союза «или», обозначается знаком «V».Характер носит разделительный.

4) Импликация, обозначается как a ® b, характер носит условный, отражает причинно-следственную связь, в речи и на письме выражается речевым клише «если, то» и прочими другими, имеющими характер причинно-следственной зависимости.

5) Эквиваленция (эквивалентность), обозначается как a º b или

a «b, характер носит тождественный, равносильный, в речи и на письме выражается речевым клише «тогда и только тогда» и прочими другими, имеющими характер равносильности и неизменности.

Исходя из значения истинности простых высказываний, можно находить значение истинности любого сложного высказывания.

Правила истинности логических связок:

Конъюнкция истинна тогда, когда оба или все ее члена истинны.

Дизъюнкция истина тогда, когда хотя бы один ее член истинен.

Импликация истина всегда, кроме тех случаев, когда следствие является ложью, а причина истинна.

Эквиваленция истинна в том случае, когда либо оба ее члена одновременно истинны, либо оба одновременно ложны.

Две формулы алгебры называют равносильными, если их таблицы истинности совпадают.

1) Переместительный закон для дизъюнкции x V y º y V x

2) Переместительный закон для конъюнкции xy º yx

3) сочетательный закон дизъюнкции (xVy)Vz º xV(yVz)

4) сочетательный закон конъюнкции (xVz) º xz V yz

5) распределенный закон дизъюнкции xyVz º (xVz)(yVz)

6) распределенный закон конъюнкции (xVy)z º xz V yz

7) закон двойного отрицания ùùx º x

8) закон равносильности де Моргана ù (xVy)º ùxùy; ù(xy) º ùx V ùy

9) исключение импликации x ® y º ù xVy

10) исключение эквивалентности x «y º (ùxVy)(xVùy)

Формула алгебры высказываний задана в дизъюктивно-конъюктивной нормальной форме (ДНФ), если она представлена в виде дизъюнкции конъюнкций элементарных высказываний и их отрицаний.

Формула алгебры высказываний задана в КНФ, если она представлена в виде конъюнкции дизъюнкций переменных и их отрицания. На основе равносильных преобразований любая формула приводима к ДНФ и КНФ с помощью следующего алгоритма:

1) избавляются от связок импликации, эквивалентности

2) приводят отрицания к независимым переменным

3) раскрывают скобки по распределенному закону для конъюнкции для приведения к ДНФ или для дизъюнкции для приведения к КНФ

4) при наличии двойных отрицаний каждый раз от них избавляются

Одна и та же формула алгебры имеет множество различных ДНФ и КНФ.