Тема 13: Логические методы принятия решений

Ключевые понятия темы: Диаграмма Исикавы (Ishicawa), метод 4-х М или метод «Рыбья» кость. Метод логической оптимизации и построение таблиц решений. Системные приоритеты.Лексеграфическое произведение чисел. Применение в менеджменте.

Диаграмма Исикавы (Ishicawa), метод 4-х М или метод «Рыбья» кость это метод японского менеджмента. Он предназначен для декомпозиции проблемы на все простые составляющие части и решение каждой из них по частям, что позволяет упростить задачу принятия решения до поэтапного сценария принятия отдельных элементов задачи.

а) Определите управленческую проблему на предприятии;

б) Произведите описательную характеристику предприятия (реального или вымышленного) в разрезе предложенной проблемы, т.е. требуется ввести данные для анализа вышеуказанной проблемы.

в) Используя метод «Диаграммы Иссикавы» проанализируйте предложенную проблему,устанавливая импликативные связи между причинами и следствиями проблемы. Данная диаграмма должна включать четыре «ММММ» по смысловой нагрузке, где 1-М-(men-люди); 2-М-(machine-оборудование);3-М-(method-метод);4-М-(material-сырьё), т.о. требуется разбить проблему на 4

(или более) кластера.

г) Данная диаграмма представляет собой графическое отображение проблемы в виде так называемой «рыбьей кости», т.е. должна иметь подобный вид:

Пример схематического отображения диаграммы Исикава:

оборудование

На заключительном этапе следует изобразить полученную диаграмму по методу Исикавы.

Нахождение логического решения. Выбор оптимального решения осуществляется путем испытания противоположных вариантов с целями. Организационное решение должно давать достижение цели в заданный срок и с минимальной затратой ресурсов.

Модель логической оптимизации решений.

Организационное решение Д* должно привести к реализации глобальной цели.

Д* ® А₀

Д* не противоречит достижению подцелей.

(Д* ® А₀ ) ^ (^ Д* А j)

j=I₁п

В качестве А может выступать комплексная цель.

А¹ и А¹¹

А¹ ^ А¹¹ ® А₀

В таком случае наша задача будет разбиваться на 3 этапа.

1 этап: нахождение решение Д*; которое позволяет достигать А¹

Д₁* ® А¹

2 этап: Д₂ * ®А¹¹

3 этап: (Д₁* ® А¹)(Д₂* ® А¹¹), Д₁*^Д₂* - не противоречат друг другу.

Задачу можно представить в виде графа целе-решений:

где А_о генеральная цель,

Аj – уровень подцелей; Д_i - решения;

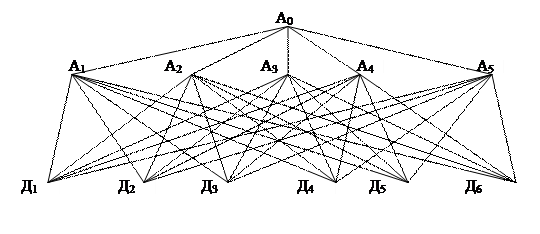
Самая приоритетная подцель с наименьшим рангом.

	А1	А2	А3	А4	А5	сумма
А1
А2
А3
А4
А5

2 – более предпочтительно

1 – совпадают (тождественно)

0 – менее предпочтительно

Предпочтение отдаем наибольшему рангу,в данном случае, это число(7) – ранг № 1 в данной таблице.

Пунктирные и сплошные связи рассматриваются отдельно, если некоторое решение Д_i несовместимо с А_j (по цели), то возникает некоторая проблема – недостижение А_j. Поэтому дается отношение достаточности – сплошные мнения и отношения несовместимости - пунктуационная линия соответственно в таблице целей нет.

+Будет обозначать достаточность, а

- несовместимость.

А₀ А₁ А₂ А₃ А₄ А₅ Таблица целерешений.

Д₁ +1 -3 +2 - 2 0

Д₂ если есть «-», то модуль вычеркиваем.

Д₃

Д₄

Д₅

Д₆

Д₇

Некоторое решение Дi характеризуется определенным количеством ресурсов

Аj и временем t_i необходимо для реализации данного решения, если реализация комплексного решения обеспечивает достижение целей.

^ Д_gh ^Дt = 1,п A_j - меторешение.

Меторешение не может существовать, если для достижения этой цели не найдется варианта, который не противоречит со всеми остальными целями. Для нахождения меторешения необходимо удалить из множества решений, те Дi, у которых есть в таблице «цели-решения» (строке), есть хотя бы 1 отрицательный элемент. Если выполнение отдельного решения может осуществляться параллельно, то время меторешения будет определяться по максимальному t_i, в противном случае время не торопиться определять как критическое время по сетевому графу реализации меторешений. Локальные приоритеты целей и решений измеряться в рангах, которые дают дополнительную инициативу, которая используется для учета специальных целей и сравнительного эффекта от реализации решений.

Локальные приоритеты могут быть определены путем анализа зависимости между реализации решений и достижением целей. При этом, чем значение локального приоритета тем больше важность.

Локальные приоритеты включают.

1) ориентировка целей принятия решений А_j по важности или по степени необходимости для достижения генеральной цели.

2) ориентировка вариантов достижения которой цели по степени достаточности Д+.

3) ориентировка решений несовместные с А_j или по степени вредности для ее достижения.

Системные приоритеты используются для комплексной оценки необходимости или вредности реализации отдельных решений. Для достижения глобальных целей системы приоритетов совпадают с локальными.

Тема 14: Метод анализа иерархии (МАИ)

Ключевые понятия темы: Варианты применения метода анализа иерархии в процессе осуществления управленческой деятельности на различных уровнях менеджмента.

Сущность метода анализа иерархии (МАИ).

МАИ является системной процедурой для иерархического представления элементов, определяется суть любой проблемы. МАИ состоит в декомпозиции проблемы на все более простые части и последние обработки последовательности (ЛПР) по парным сравнениям с исполнением шкалы от 1 до 9. В результате может быть численно выражена относительная степень взаимодействия элементов в иерархии. Решение проблемы есть процесс поэтапного установления приоритетов.

1) выявленные наиболее важных элементов проблемы.

2) оценка элементов.

3) выработка способов применения решений и оценка его качества.

Метод позволяет в качестве исходного материала использовать субъективные оценки, следовательно, он исходит из способности людей мыслить творчески и получить ясное представление о своем внутреннем потенциале.

Принципы МАИ.

1) Принцип декомпозиции - предусматривает конструкцию проблемы, в виде иерархии, начиная с вершины (целей с точки зрения управления) через промежуточные уровни (критерии, от которых зависят последующие уровни) к самому низшему уровню, (который обычно состоит из альтернатив).

Проблема

Критерии уровень 1

А₁ А₂ А_п уровень 2

Альтернативы

А Б М уровень 3

Если число критерий большое их может объединять в кластеры, которые образуют свой уровень.

2) Принцип сравнительных суждений.

Закон иерархической непрерывности требует, чтобы элементы нижнего уровня иерархии были сравнимы попарно по отношению к элементам следующего уровня и так далее, вплоть до вершины иерархии. Сравнивая набор составляющих проблемы друг с другом, по отношению к их воздействию («вес или интенсивность») на общую для них характеристику, получаем квадратную матрицу.

А₁₁ а_{12………..}а_1п а_ij=1/a_ji - это матрица имеет свойство обратной симметричности.

А₂₁а_22………а_2п

_{……………………..} i – номер строки

_{…………………….} J – номер столбца

а_п1 а_п2……а_пп

Если а_ij не известны заранее, то парные сравнения производятся с использованием субъективных суждений мысленно оценивая их по шкале 1 – 9. Каждая проблема представляется иерархически.

1. для сравнения относительной важности критериев на 2-ом уровне по отношению в общей цели на1-ом уровне.

2. для парных сравненных альтернатив на 3-м уровне по отношению к каждому критерию 2-го уровня, то есть для иерархии изображена на рис.1 потребуется построить n+1 матрицу.

3. Шкала сравнения 1-9.

Интенсивность

Относительной Определение

Важности

1 равная важность

3 умеренное превосходство

5 существенное или сильное превосходство

7 значительное превосходство

9 очень сильное превосходство

2, 4, 6, 8 они означают промежуточные, компромисс или «обратные»

Схема вычисления согласованности.

А₀ А₁ А₂…….А _п

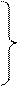
А₁ а₁₁ а₁₂…..а_{1 п} (а₁₁+а _п +…..+а _{п 1})х₁ = λ₁

А₂ а₂₁а₂₂…..а_{2 п} (а₁₂+а₂₂+….+а _{п 2})х₂ = λ ₂ 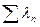= λ _мах

……………………

А_п а _{п 1} а _{п 2}…..а _пп (а _{п 1}+а _{п 2}+….+а _пп)х _п = λ _п

…

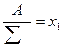
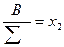
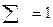
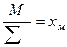
ИС=(λ(мах)- п), где п -1 ОС= ИС 100 %

п -1 ОС

Размер матрицы	п
СС	СС			0,58	0,90	1,12	1,24	1,32	1,41	1,45	1,49

VI. Принцип синтеза глобального приоритета.

Приоритеты синтезируются со 2-го уровня. В них локальные приоритеты перемножаются на локальный приоритет и суммируются по каждому элементу в соответствии с критериями.

Это дает составной или глобальный приоритет того элемента, который далее исполняется для взвешивания локальных приоритетов элементов, сравниваемых по отношению к нему, как к критерию, и расположенному уровнем ниже.

Процедура продолжается до самого нижнего уровня.

Схема.

У_j={х_1а…х_1к }х₁+{х_2а…х_2к}х₂+…+{х_па...х_пв}х_п, гдеj=А, Б, К

VII. Выбор решения. Сравниваем глобальные приоритеты альтернатив, показывающие отношению к проблеме. Делаем выбор решения: у_j=max.

VIII. Согласованность иерархии. Для этого перемножаем индекс согласованности на приоритет соответствующего критерия и суммируем полученные числа.

Результат делим на соответствующую величину СС, согласно таблице значений случайной согласованности.

Тема 15: Эвристические методы синтеза системы

Ключевые понятия темы: Классификация эвристических методов синтеза. Методы ненаправленного синтеза решения.Метод аналогии. Метод инверсии. Метод эмпатии. Метод идеализации. Методы направленного синтеза решений. Способы применения методов при PR-менеджменте, рекламном менеджменте и пр.

Под эвристическим синтезом понимается способ решения какой-либо поставленной задачи, включающий совокупность приемов мыслительной деятельности, а также операций по сбоку, анализу, обработке и хранению информации. Эвристические методы синтеза используются при необходимости поиска как можно большего числа новых рациональных решений для реализации полезных функций системы, для устранения или ослабления отрицательного эффекта ненужных и излишних функций, для эффективного синтеза новых или рациональных систем.

Эвристические методы синтеза направлены на реализацию эффективных решений, отвечающих современному уровню развития науки, экономики и систем управления и т.п., за счет увеличения функционально взаимозаменяемых вариантов, позволяющих приблизить синтезируемую систему к минимальным, функционально оправданным затратам.

Эвристический синтез базируется на эвристике – науке о творческом мышлении. Кроме того, используются положения таких наук, как психология творчества, системный анализ, исследование операций, теория игр, праксеология и др. Эвристический синтез нередко приводит к получению принципиально новых решений.

В России и за рубежом разработано большое число методов эвристического синтеза для решения задач в различных областях – технике, экономике, управлении, дизайне и др. В этой главе будут даны те эвристические методы, которые наиболее удачно могут быть применены для поиска эффективных экономических, управленческих и организационных решений.

Наиболее значимым признаком классификации методов эвристического синтеза является наличие или отсутствие алгоритма, организующего мыслительный процесс. По этому признаку можно выделить две группы методов: методы ненаправленного (полуупорядоченного) синтеза, опирающиеся только на простейшие приемы ассоциативного мышления; методы направленного (упорядоченного) синтеза, для которых характерны комплексный подход, системный анализ проблемы и алгоритмизация творческого процесса.

Методы ненаправленного синтеза решения

К методам ненаправленного синтеза решений относятся следующие приемы творчества: аналогия, инверсия, эмпатия, идеализация.

Метод аналогии предусматривает использование подробного (аналогичного) известного решения, которое «подсказано», например, литературой по экономике, менеджменту, изобразительному искусству или «подсмотрено» в природе.

Для освоения этого метода необходимо обладать (и развивать) наблюдательностью и способностью к переносу опыта.

Метод инверсии основан на использовании при решении задачи принципов перестановки, переворачивания, выворачивания на изнанку. Этот метод приучает к гибкости мышления, отказу от традиционных стереотипных решений, преодолению психологической инерции.

Метод эмпатии означает отождествление себя с разрабатываемой системой. При этом исследователь как бы ставит себя на место, например, банка, рекламы, товара и стремится ощутить все действия, которые над ним могут совершаться.

Метод идеализации связан с желанием получить представление об идеальной системе, полностью отвечающей поставленной цели. Рассматривать идеальные решения часто оказывается полезным, даже если это сопряжено с определенной долей фантазии, поскольку такие решения могут натолкнуть на новую идею

Наиболее эффективны для синтеза новых решений методы направленного синтеза, основанные на научно обоснованных алгоритмах творческого процесса. На одних этапах алгоритмов поле поиска расширяется, на других – сужается. Указанные алгоритмы не имеют жесткой структуры и зачастую называются эвристическими алгоритмами.

Для предания процессу синтеза общей направленности требуется четкая постановка цели и уяснение сущности решаемой задачи. Для этого целесообразно использовать понятия экономического, управленческого или организационного противоречия и идеального конечного результата. Экономическое, управленческое или организационное противоречие характеризует несоответствие между возникшими потребностями общества и возможностями существующих систем. В более узком смысле указанные виды противоречий проявляются при улучшении одних характеристик, рассматриваемых систем, повлекшем за собой ухудшение других характеристик.

Идеальный конечный результат (ИКР) – это гипотетическое идеализированное решение, к которому следует стремиться и которое соответствует поставленной цели. ИКР является своего рода критерием синтеза и выбора решений, в соответствии с которым лучшим считается решение, наиболее близкое к ИКР. При использовании ИКР задача рассматривается только с потребительской стороны и поэтому не может заменить социально-экономические оценки вариантов, характеризующие их эффективность.

Современные методы направленного синтеза основаны на сложных алгоритмизированно-процедурных подходах, типизированных способах решения разнообразных изобретательских задач.

СПИСОК ИСПОЛЬЗОВАННЫХ ЛИТЕРАТУРНЫХ ИСТОЧНИКОВ

1. Античные риторики. М., 1978.

2. Аристотель. Соч.: В 4 т. М., 1975-1978.

3. Асмус В.Ф. Логика. М., 1947; он же. Учение логики о доказательстве и опровержении. М., 1954.

4. Бочаров В. А., Маркин В. И. Основы логики. — М.: Космополис, 1994.

5. Бэкон. Соч. В 2 т. М. 1977—1978.

6. Великие мысли великих людей. Антология афоризма: В 3 т. М., 1998.

7. Галкин Е. В. Нестандартные задачи по математике. М.: Просвещение; Учебная литература, 1996.

8. Гегель Г. Работы разных лет. Т. 1—2. М., 1970—1971.

9. Гетманова А. Д. Учебник по логике. — М., 1994.

10. Градштейн И. С. Прямая и обратная теоремы. — М.: Наука, 1972.

11. Зейгарник Б.В. Патопсихология. М., 1976.

12. Ивин А. А. Искусство правильно мыслить. — М.: Просвещение, 1990.

13. Ивин А. А. Логика. — М.: Просвещение, 1996.

14. Ивлев Ю. В. Логика. — М.: Логос, 1997.

15. Игошин В. И. Математическая логика и теория алгоритмов. - Саратов: Издательство Саратовского университета, 1991.

16. Игошин В. И. Задачник-практикум по математической логике. М.: Просвещение, 1986.

17. Кейслер Г., Чен Ч. Теория моделей. – М.: Мир, 1977.

18. Кириллов В. И., Старченко А. А. Логика. — М.: Юрист, 1993.

19. Курбатов В. И. Логика. — Ростов-на-Дону: Феникс, 1997.

20. Клини С.К. Математическая логика. М., 1973.

21. Кондаков Н. И. Логический словарь-справочник. — М.: Наука, 1975.

22. Лавров И. А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов.- М.: Наука, 1975.

23. Лихтарников Л. М., Задачи мудрецов: Книга для учащихся. - М.: Просвещение: АО "Учебная литература", 1996.

24. Мальцев А.И. Алгоритмы и рекурсивные функции. - М.: Наука, 1965.

25. Математическая логика (Под общей редакцией А. А. Столяра и др.). - Минск: Высшая школа, 1991.

26. Мендельсон Э. Введение в математическую логику. - М.: Наука, 1976.

27. Милль Дж. Ст. Система логики силлогистической и индуктивной. М., 1914.

28. Минто В. Дедуктивная и индуктивная логика. М., 1901.

29. Михаилов А. Б., Плоткин А. И. Введение в алгебру и математический анализ. Сборник задач 1. Высказывания. Предикаты. Множества. - Санкт-Петербург, 1992.

30. Нестеренко Ю. В. и др. Лучшие задачи на смекалку. — М.: АСТ-ПРЕСС, 1999.

31. Новиков П. С. Элементы математической логики. - М.\ Наука, 1973.

32. Панасюк А. Ю. Как победить в споре, или искусство убеждать. — М.: Олимп; ACT, 1998.

33. Поварнин С. И. Спор. — СПб, 1996.

34. Плеханов Г.В. Избр. филос. произв.: В 5 т. М., 1956—1958.

35. Упражнения по логике. / Под ред. В. И. Кириллова. - М.: Юрист, 1993

36. Федеральный закон «О международных договорах Российской Федерации» №101 ФЗ от 15.07.95.

37. Федеральный закон «О профессиональных союзах, их правах и гарантиях деятельности» №10 ФЗ от 12.01.96.

38. Хоменко Е. А. Логика. — М., 1976.

39. Челпанов Г.И. Учебник логики. М., 1996.

40. Черч А. Введение в математическую логику.-М.: Мир, 1960.

41. Экономика. М., 1996.

42. Энгельс Ф. Анти-Дюринг. — Маркс К., Энгельс Ф. Соч. Т. 20.

43. Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста. - М.: Наука, 1966.