Закон возрастания энтропии

На основе неравенства Клаузиуса (10) можно доказать следующую важную теорему: энтропия полностью изолированной системы ни при каких процессах не может убывать; она либо остаётся постоянной, если процесс обратим, либо возрастает, если в нём есть необратимые стадии:

Δ S ₁₂= S ₂− S ₁≥0, т.е. S ₂≥ S ₁ (без доказательства).

Это утверждение носит название закона возрастания энтропии.

Замечание 1. Неравенство Δ S ≥0 применимо только к полностью изолированным системам. Если система не является изолированной, то её энтропия может и убывать в любых процессах, но энтропия внешней среды при этом возрастает на столько же, или ещё больше.

Замечание 2. Формула (12) даёт термодинамическое определение энтропии, из которого не вполне понятен её физический смысл. Этот смысл проясняется из статистического толкования энтропии:

S = k ln N,

где k – постоянная больцмана, N – число микросостояний системы, которыми реализуется её данное макросостояние, характеризующееся параметрами p, V, Т.

Пример. Тепловой контакт двух тел с разными температурами Т ₁ и Т ₂ приводит к необратимому процессу теплопередачи.

Пусть горячий камень с температурой Т ₂ бросили в холодную воду с температурой Т ₁. Камень отдаёт воде тепло Δ Q при своей температуре Т ₂> Т ₁, следовательно, его энтропия изменяется на величину Δ S ₂=−Δ Q / Т ₂ (убывает). Вода поглощаетто же тепло, но уже при своей температуре Т ₁< Т ₂, следовательно, её энтропия изменяется на величину Δ S ₁=+Δ Q / Т ₁ (возрастает). Тогда общее изменение энтропии системы «вода-камень»:

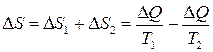>0.