Постановка задачи. пусть требуется вычислить

пусть требуется вычислить 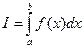. Из курса математического анализа известно, что если функция 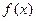непрерывна на отрезке 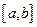и известна ее первообразная, 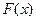, то интеграл от функции 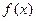можно вычислить по формуле Ньютона-Лейбница

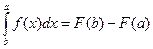, где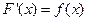

Однако это не всегда возможно, например, 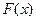не выражается через элементарные функции в конечном виде или выражается в конечном виде, но имеет сложный вид и вычислений значений функци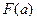и и 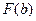затруднительно.

Если же 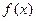- непрерывна, но задана таблицей, то формулу Ньютона-Лейбница вообще применить нельзя.

В таких случаях ставится задача приближенного вычисления интеграла с помощью численных методов.

Задача численного интегрирования фактически заключается в вычислении значения определенного интеграла на основании ряда значений подынтегральной функции.

Суть большинства методов численного интегрирования состоит в замене подынтегральной функции 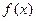интерполяционным многочленом, например, Лагранжа или Ньютона.

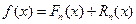
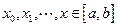- узлы интерполирования

Тогда

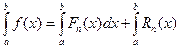
Оба интеграла справа существуют, тогда приближенно можно принять

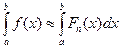(1)

А погрешность

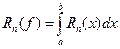(2)

Формула (1) и называется формулой численного интегрирования.

Формулы численного интегрирования называют также квадратными формулами.