При построении ДУ, реализующих заданные логические функции, возникает задача нахождения таких форм функций, для реализации которых требуется минимальное количество логических элементов из заданного перечня.
Процесс преобразования логических функций, при котором находится наиболее простое их представление, содержащее наименьшее число входящих в них символов аргументов (букв), называется минимизацией.
Сложность логической функции оценивается общим числом входящих в нее букв, а не переменных, считая различными буквами вхождение одной и той же буквы в различные дизъюнктивные (конъюнктивные) члены функции.
Так, например, функция 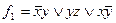 содержит 6 букв, а функция
содержит 6 букв, а функция 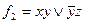 – 4 буквы, хотя и та и другая зависят от трех переменных x, y, z.
– 4 буквы, хотя и та и другая зависят от трех переменных x, y, z.
Методы минимизации логических функций, известные в настоящее время, разработаны применительно к задаче получения формул минимальной сложности (длины). Критерием минимизации здесь является количество букв, входящих в алгебраическое выражение заданной функции. Формуле минимальной длины всегда соответствует релейно-контактная схема с минимальным количеством исполнительных органов (контактов). Сложность схем из бесконтактных логических элементов определяется количеством входов и выходов в элементах схемы. А так как каждая буква в формуле – это вход на схеме, то и здесь формуле минимальной длины соответствует более простая схема, так как число p - n -переходов в ИМС не лимитируется.
|
|
|
Мы рассмотрим минимизацию логических функций в классе дизъюнктивных нормальных форм. Именно такая форма является наиболее употребительной, и, кроме того, любая логическая функция легко может быть представлена в ДНФ. Однако минимизация функций в классе КНФ принципиально ничем не отличается от минимизации в классе ДНФ и также вполне возможна с небольшими изменениями производимых операций (вспомним, что все законы алгебры логики являются двойственными).
Сущность минимизации логической функции, заданной в СДНФ, заключается в том, что получают ДНФ заданной функции путем группировки соседних, отличающихся друг от друга значением только одной переменной членов (конституент) СДНФ и исключением одной переменной по соотношению 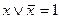 (по закону склеивания).
(по закону склеивания).
Описанная операция носит название склеивания. После нее производят упрощения по закону повторения. Этот процесс попарного склеивания повторяют до тех пор, пока в полученном выражении не останется конъюнкций, отличающихся значением одной переменной. Получают минимизированную логическую функцию, например:
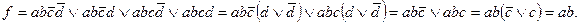
Однако такая минимизация СДНФ методом непосредственного упрощения, т.е. попарного склеивания, является чрезвычайно громоздкой операцией и для сложных функций вообще не приемлема.
|
|
|
В настоящее время разработаны различные методы минимизации логических функций, позволяющие избежать громоздкости. Рассмотрим некоторые из них:
1. Минимизация таблично-аналитическим методом (методом Квайна и Квайна – Мак-Класки).
2. Минимизация с помощью карт Карно.
3. Минимизация на основе использования решетки соседних чисел и обобщенных кодов (метод Л. Т. Мавренкова).
4. Минимизация, основанная на использовании поразрядного сравнения рабочих и запрещенных наборов и восьмеричной системы счисления (метод Л. Ф. Викентьева).
5. Минимизация, основанная на поразрядном сравнении рабочих и запрещенных обобщенных кодов (метод Л. Ф. Викентьева).
Предварительно введем несколько очень важных для процесса минимизации определений.
Логическая функция 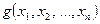 называется импликантой логической функции
называется импликантой логической функции 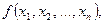 если на любом наборе значений переменных
если на любом наборе значений переменных 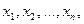 на котором значение функции
на котором значение функции 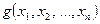 равно 1, значение функции
равно 1, значение функции 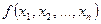 также равно 1.
также равно 1.
Совершенно очевидно, что для функции, записанной в СДНФ, любой член СДНФ (конституента) является импликантой.
Для функции 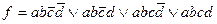 функция
функция 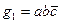 является импликантой, так как функция
является импликантой, так как функция 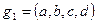 равна 1 на наборах переменных 1100 и 1101; на этих же наборах равна 1 и функция f.
равна 1 на наборах переменных 1100 и 1101; на этих же наборах равна 1 и функция f.
Простой импликантой функции f (x) называется элементарная конъюнкция g (x), являющаяся импликантой этой функции и обладающая тем свойством, что никакая ее собственная часть, т.е. конъюнкция, получаемая из элементарной путем исключения одной или нескольких переменных, уже не является импликантой данной функции.
Конъюнкция g 2 = ab представляет собой простую импликанту для функции f, так как g 2 = 1 на наборах 1100, 1101, 1110, 1111 и f = 1 на тех же наборах и, кроме того, ни функция g 3 = a, ни функция g 4 = b уже не являются импликантами функции f.
Очевидно, что импликанта 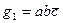 не является простой, так как полученная из нее функция g 2 = ab сама является импликантой.
не является простой, так как полученная из нее функция g 2 = ab сама является импликантой.
Видно, что импликанты логической функции получаются при выполнении операции склеивания некоторого множества конституент, а простые импликанты – в результате многократного повторения операции склеивания, когда оставшиеся члены ДНФ больше не являются соседними и дальнейшему склеиванию не поддаются.
Импликанта, полученная в результате склеивания некоторого множества конституент, покрывает эти конституенты. Так, в нашем примере импликанта  покрывает конституенты
покрывает конституенты 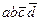 и
и 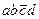 исходной функции, а импликанта abc – конституенты
исходной функции, а импликанта abc – конституенты 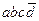 и abcd. Простая импликанта ab покрывает все четыре конституенты исходной функции.
и abcd. Простая импликанта ab покрывает все четыре конституенты исходной функции.
Легко доказать, что дизъюнкция всех импликант логической функции совпадает с самой функцией, т.е. равносильна ей.
Дизъюнкция всех простых импликант логической функции называется сокращенной дизъюнктивной нормальной формой этой функции (СкДНФ). Пусть задана логическая функция
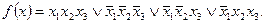
Определим все простые импликанты для этой функции путем попарного сравнения и склеивания каждой конституенты со всеми последующими. Получим простые импликанты функции f (x):
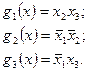
Других простых импликант у данной функции нет. Поэтому сокращенная ДНФ для этой функции имеет вид:
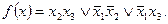
Так как СкДНФ функции есть дизъюнкция всех простых импликант, то представление любой логической функции в СкДНФ является единственным.
Очевидно, что СкДНФ содержит меньшее число переменных, чем СДНФ, но она отнюдь не является минимальной и в большинстве случаев допускает дальнейшее упрощение за счет того, что некоторые из простых импликант могут поглощаться дизъюнкциями других простых импликант (по закону обобщенного склеивания).
В рассмотренном примере импликанта 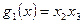 покрывает конституенты
покрывает конституенты 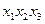 и
и 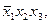 импликанта
импликанта 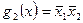 – конституенты
– конституенты 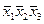 и
и 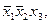 импликанта
импликанта 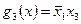 – конституенты
– конституенты 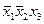 и
и 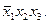
Видим, что конституенты 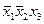 и
и 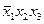 покрываются дважды, что, очевидно, является избыточным.
покрываются дважды, что, очевидно, является избыточным.
|
|
|
Система (совокупность) импликант называется полной, если каждая конституента (единичное значение) исходной функции покрывается хотя бы одной импликантой системы.
В нашем примере система, состоящая из трех импликант – 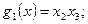
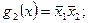
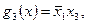 является полной для исходной функции. Очевидно, что система, состоящая из двух импликант –
является полной для исходной функции. Очевидно, что система, состоящая из двух импликант – 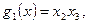
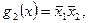 также является полной, покрывающей все конституенты исходной функции. Исключение импликанты
также является полной, покрывающей все конституенты исходной функции. Исключение импликанты 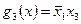 не нарушило полноты системы, исключение же любой другой импликанты нарушит полноту системы.
не нарушило полноты системы, исключение же любой другой импликанты нарушит полноту системы.
Система простых импликант логической функции называется приведенной, если она полна и исключение из нее хотя бы одной импликанты нарушает эту полноту.
Так система импликант 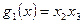 и
и 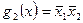 является приведенной.
является приведенной.
Дизъюнкция простых импликант, составляющих приведенную систему импликант функции, называется ее тупиковой дизъюнктивной нормальной формой (ТДНФ).
Для нашего примера ТДНФ имеет вид:
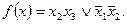
В общем случае, логическая функция может иметь несколько тупиковых ДНФ.
Тупиковая ДНФ логической функции, содержащая наименьшее число букв (символов переменных), называется минимальной дизъюнктивной нормальной формой (МДНФ).
Отметим, что полученная в примере единственная ТДНФ, очевидно, является и МДНФ.
Минимальная ДНФ функции, найденная путем построения и перебора всех тупиковых ДНФ и выбора из них самой минимальной, называется общей (абсолютной) минимальной ДНФ.
При решении практических задач часто затруднительно отыскать все тупиковые ДНФ логической функции. Поэтому, чтобы сократить объем работы, ограничиваются нахождением одной или нескольких ТДНФ, из которых выбирают минимальную. Такие минимальные ДНФ называются частными дизъюнктивными нормальными формами.
Получив частную минимальную ДНФ (одну из ТДНФ), считают ее близкой к общей МДНФ, что, вообще говоря, не всегда является верным.
Особенно большое отличие по количеству букв частных МДНФ (ТДНФ) от общей МДНФ наблюдается при решении задач синтеза ДУ по не полностью определенным логическим функциям, которые в процессе минимизации доопределяются за счет условных наборов переменных. Поэтому следует выбирать такой способ доопределения, который ведет к получению наиболее близкой к минимальной ТДНФ.
|
|
|
Следовательно, задача минимизации логических функций подразделяется на два этапа.
На первом этапе находятся все простые импликанты заданной логической функции, т.е. строится сокращенная дизъюнктивная нормальная форма.
На втором этапе определяются все приведенные системы простых импликант, строятся тупиковые ДНФ, из числа которых отбираются минимальные ДНФ логической функции.
 2014-02-13
2014-02-13 3033
3033
