Основные законы алгебры логики являются двойственными: относительно логического сложения и относительно логического умножения. Ими являются:
1. Переместительный (коммутативный) закон:
- относительно сложения
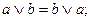
- относительно умножения
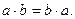
2. Сочетательный (ассоциативный) закон:
- относительно сложения
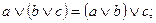
- относительно умножения
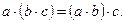
3. Распределительный (дистрибутивный) закон:
- относительно сложения
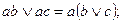
- относительно умножения
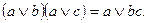
4. Закон инверсии (де Моргана):
- относительно сложения
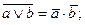
- относительно умножения
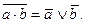
5. Закон повторения (идемпотентности):
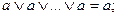
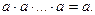
|
6. ЗакоПереместительный (коммутативный) закон:
7. Сочетательный (ассоциативный) закон:
8. Распределительный (дистрибутивный) закон:
9. Закон инверсии (де Моргана):
10. Закон повторения (идемпотентности):
6.Закон поглощения:
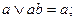
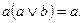
7.Закон склеивания:
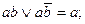
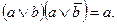
8. Закон обобщенного склеивания:
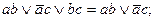
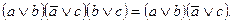
Кроме перечисленных законов большое значение в алгебре логики имеют так называемые соотношения 0 и 1. Напомним, что в алгебре логики символом 1 обозначается всегда истинное суждение (есть сигнал), а символом 0 – всегда ложное суждение (нет сигнала).
На основании алгебры логики очевидны следующие соотношения (аксиомы алгебры логики):
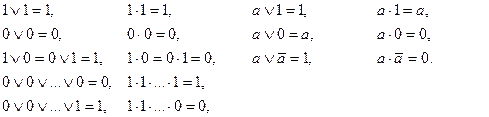
Последние соотношения (относительно a) легко доказываются подстановкой вместо a его возможных значений – 0 и 1.
Рассмотренные законы применимы не только к отдельным переменным, но и к группам переменных, объединенных операциями алгебры логики.
В алгебре логики установлен порядок выполнения действий. При отсутствии в выражении скобок первыми должны выполняться операции отрицания (инверсии), затем операции конъюнкции и последними – операции дизъюнкции. При наличии в выражении скобок в первую очередь производятся операции внутри скобок.
При преобразовании логических функций зачастую приходится производить операцию инверсирования их.
Логическая функция 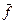 будет инверсной по отношению к функции f, если соблюдаются два соотношения:
будет инверсной по отношению к функции f, если соблюдаются два соотношения:
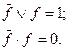
Следовательно, если на каком-либо наборе переменных функция f принимает значение 0, то функция 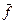 равняется 1 и наоборот.
равняется 1 и наоборот.
Для контактных схем это означает, что если при данном состоянии реле цепь, соответствующая f, замкнута, то цепь, соответствующая 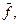 – разомкнута и наоборот.
– разомкнута и наоборот.
Под инверсированием (логическим отрицанием) функции f понимается нахождение функции 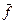 , удовлетворяющей указанным соотношениям.
, удовлетворяющей указанным соотношениям.
На основании законов инверсии можно сформулировать следующий порядок инверсирования булевых функций, записанных в базисе И, ИЛИ, НЕ.
При инверсировании булевой функции все знаки дизъюнкции заменяются на знаки конъюнкции и наоборот – при одновременном инверсировании каждого элемента. При этом для сохранения последовательности действий необходимо соответствующим образом вводить или исключать скобки.
Другими словами, логическое инверсирование производится на основе закона инверсии, который последовательно применяется к отдельным частям функции в порядке, указанном логическими операциями и определяемом самой функцией. Например, дана функция 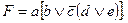 Найти
Найти 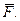
Очевидно, 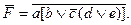 F – конъюнкция a и
F – конъюнкция a и 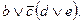 Значит, первым применяем закон инверсии относительно умножения, далее – относительно сложения во второй части и т.д.:
Значит, первым применяем закон инверсии относительно умножения, далее – относительно сложения во второй части и т.д.:

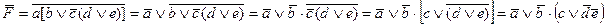
Итак, 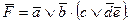
 2014-02-13
2014-02-13 6417
6417
