Малая выборка

Уточненные данные учета коммерческих палаток в районах города

Количество коммерческих палаток в районах города до и после контрольных обходов

Районы	Зарегистрировано при сплошном учете	Установлено при контрольном обходе	Коэффициент недоучета
А Б В			1,050 1,033 1,067

Рассчитанный по каждой категории работников коэффициент недоучета является основой уточнения имеющихся данных.

В нашем примере количество коммерческих палаток (по данным сплошного учета) следует умножить на рассчитанный для каждого района коэффициент недоучета. В итоге получим результаты, представленные в таблице 8.5.

Таблица 8.5.

	Количество коммерческих палаток в районах города
	А	Б	В
Данные сплошного наблюдения Численность с поправкой на недоучет

В практике статистического исследования в условиях рыночной экономики все чаще приходится сталкиваться с небольшими по объему так называемыми малыми выборками. Под малой выборкой понимает­ся такое выборочное наблюдение, численность единиц которого не пре­вышает 30. В настоящее время малая выборка используется более широ­ко, чем раньше, прежде всего за счет статистического изучения деятель­ности малых и средних предприятий, коммерческих банков, фермерских хозяйств и т.д. Их количество в определенных случаях, особенно при ре­гиональных исследованиях, а также величина характеризующих их по­казателей (например, численность занятых) часто незначительны. По­этому хотя общий принцип выборочного обследования (с увеличением объема выборки повышается точность выборочных данных) остается в силе, иногда приходится ограничиваться малым числом наблюдений. Наряду со статистическим изучением рыночных структур эта необходи­мость возникает при выборочной проверке качества продукции, в науч­но-исследовательской работе и в ряде других случаев.

При оценке результатов малой выборки величина генеральной дисперсии в расчетах не используется. Для определения возможных пределов ошибки пользуются так называемым критерием Стьюдента, определяемым по формуле:

,

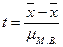где 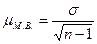- мера случайных колебаний выборочной средней в малой выборке.

Приведем выдержку из таблицы распределения Стьюдента.

Таблица 8.6.

Распределение вероятности в малых выборках в зависимости от коэффициента доверия t и объема выборки n*

t n										∞
0,5 1,0 1,5 2,0 2,5 3,0

*При n = ∞ в таблице даны вероятности нормального распределения. Для определения вероятности соответствующие табличные значения следует разделить на 1000.

Как видно из таблицы, при увеличении n это распределение стремится к нормальному и при n = 20 уже мало от него отличается.

Покажем, как пользоваться таблицей распределения Стьюдента.

Пример 9. Предположим, что выборочное обследование 10 рабочих малого предприятия показало, что на выполнение одной из производственных операций рабочие затрачивали времени (мин.): 3,4; 4,7; 1,8; 3,9; 4,2; 3,9; 4,2; 3,9; 3,7; 3,2; 2,2; 3,9. Найдем выборочные средние затраты:

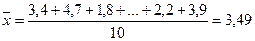мин.

Выборочная дисперсия:

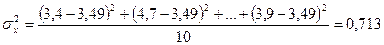
Отсюда средняя ошибка малой выборки равна:

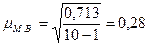мин.

По таблице 8.6. находим, что для коэффициента доверия t = 2 и объема малой выборки n = 10 вероятность равна 0,924. Таким образом, с вероятностью 0,924 можно утверждать, что расхождение между выборкой и генеральной средними лежит в пределах от 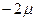до 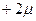, т.е. разность 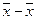не превысит по абсолютной величине 0,56 (2×0,28). Следовательно, средние затраты времени по всей совокупности будут находится в пределах от 2,93 до 4,05 мин. Вероятность того, что это предположение в действительности неверно и ошибка по случайным причинам будет по абсолютной величине больше, чем 0,56, равна: 1-0,924 = 0,076.