Рассмотрим большие выборки (порядка сотен наблюдений).
Теорема. Вероятность того, что отклонение выборочной средней (или доли) от генеральной средней (или доли) не превзойдёт по абсолютной величине число 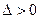 , равна:
, равна:
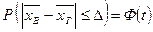 ,
, 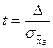 ;
;
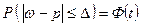 ,
, 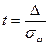 . -
. -
формулы доверительной вероятности для средней и доли.
Где 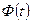 - функция Лапласа,
- функция Лапласа, 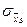 и
и 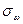 - среднеквадратические отклонения выборочной средней и выборочной доли или среднеквадратические ошибки выборки (собственно случайная повторная выборка). Если выборка бесповторная, то среднеквадратические отклонения выборочной средней и выборочной доли -
- среднеквадратические отклонения выборочной средней и выборочной доли или среднеквадратические ошибки выборки (собственно случайная повторная выборка). Если выборка бесповторная, то среднеквадратические отклонения выборочной средней и выборочной доли - 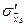 и
и 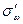 .
.
| Повторная выборка | Бесповторная выборка | |
| Средняя | 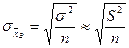 | 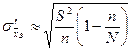 |
| Доля | 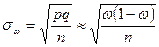 | 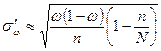 |
Формулы для нахождения среднеквадратических ошибок выборки запишем в таблицу.
При малом объеме выборки  величина
величина 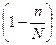
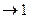 , поэтому значения для среднеквадратических ошибок при повторной и бесповторной выборке приблизительно равны между собой.
, поэтому значения для среднеквадратических ошибок при повторной и бесповторной выборке приблизительно равны между собой.
Следствия теоремы:
1) при заданной доверительной вероятности 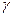 предельная ошибка выборки
предельная ошибка выборки
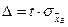 ,
,
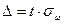 , где
, где 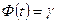 .
.
2) доверительные интервалы для генеральной средней и генеральной доли могут быть найдены по формулам
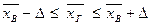 ,
,
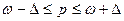 .
.
Пример 9.1. Для определения средней урожайности пшеницы на площади 10000 Га определена урожайность на 1000 Га. Результаты выборки приведены в таблице:
| Урожайность, ц/Га | 11-13 | 13-15 | 15-17 | 17-19 |
| Количество, Га |
Найти:
1) вероятность того, что средняя урожайность пшеницы на всём массиве отличается от средней выборочной не более чем на 0,1 ц, если выборка:
а) повторная;
б) бесповторная;
2) границы, в которых с вероятностью 0,9973 заключена средняя урожайность на всём массиве.
Решение. Вычислим выборочную среднюю и выборочную дисперсию.
Середины интервалов равны: 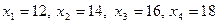 .
.
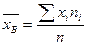
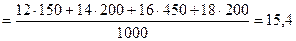 ц.
ц.
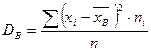 ,
,
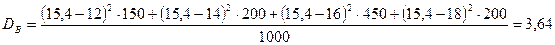
1) Запишем формулу доверительной вероятности для выборочной средней
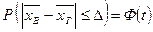 .
.
а) Если выборка повторная, то 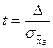 , где
, где 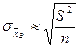 ,
, 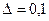 .
.
Найдем 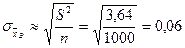 . Т.о.
. Т.о. 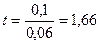 , а доверительная вероятность
, а доверительная вероятность
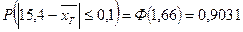 .
.
б) Если выборка бесповторная, то 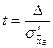 , где
, где 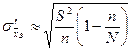 .
.
Найдем 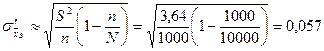 .
.
Т.о. 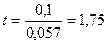 , а доверительная вероятность
, а доверительная вероятность
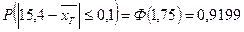 .
.
2) Средняя урожайность на всём массиве заключена в границах:
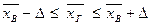 .
.
По условию 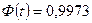
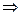
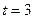
Предельная ошибка выборки: 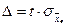
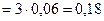 ц. – выборка повторная,
ц. – выборка повторная,
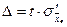
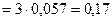 ц. – выборка бесповторная.
ц. – выборка бесповторная.
Таким образом с вероятностью 0,9973 средняя урожайность на всём массиве заключена в границах: 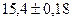 , т.е.
, т.е. 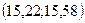 - выборка повторная,
- выборка повторная,
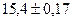 , т.е.
, т.е. 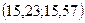 - выборка бесповторная.
- выборка бесповторная.
9.3. Объём выборки
Для проведения выборочного наблюдения важно правильно установить объём выборки  при заданных величинах надёжности оценки
при заданных величинах надёжности оценки 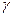 и точности оценки
и точности оценки 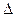 . Объём выборки находится из формул предельной ошибки выборки:
. Объём выборки находится из формул предельной ошибки выборки: 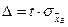 - при оценке генеральной средней или
- при оценке генеральной средней или 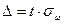 - при оценке генеральной доли.
- при оценке генеральной доли.
Формулы для нахождения объема выборки представлены в таблице.
| Повторная выборка | Бесповторная выборка | |
| Средняя | 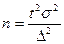 | 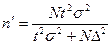 |
| Доля | 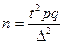 | 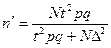 |
Если найден объём повторной выборки  , то объём бесповторной выборки
, то объём бесповторной выборки 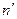 можно определить по формуле
можно определить по формуле
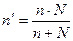 .
.
Так как 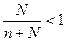 , то
, то 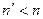 .
.
Пример 9.2. По условию примера 9.1. определить объём выборки, при котором с вероятностью 0,9973 отклонение средней урожайности в выборке от средней урожайности на всей площади посева не превзойдет 0,5 ц (по абсолютной величине).
Решение. Если выборка повторная, то ее объем 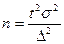 .
.
В качестве 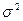 берём состоятельную оценку
берём состоятельную оценку 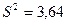 ;
;
так как 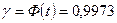
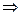 по таблице
по таблице 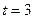 . Таким образом
. Таким образом 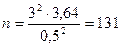 .
.
Объем бесповторной выборки 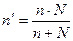
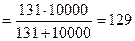 .
.
 2014-02-09
2014-02-09 5105
5105

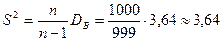 .
.