Кратномасштабный анализ (КМА) основывается на представлении сигнала на основе суммирования его грубого представления с детализирующими локальными представлениями сигнала в его разных местах. Для этого используют ортогональные вейвлеты, создавая их на представлении пространства V в виде системы вложенных подпространств Vj, отличающихся друг от друга только перемасштабированием независимой переменной.
Этот вид анализа базируется на следующих исходных предпосылках:
● пространство сигналов V может быть разбито на иерархически вложенные подпространства Vj, которые не пересекаются и объединение которых дает в пределе L ²(R);
● для любой функции s (t)Î Vj ее сжатая версия принадлежит пространству Vj-1;
● существует такая функция φ (x)Î V 0, для которой ее сдвиги
φ 0, j = φ (t-k) при k 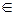 Z образуют ортонормированный базис пространства V 0.
Z образуют ортонормированный базис пространства V 0.
Так как функции φ0,k (t) образуют ортонормированный базис пространства V 0, то функции
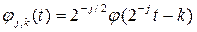 (8)
(8)
образуют ортонормированный базис пространства Vj.
Эти функции называются масштабирующими, потому что они создают свои масштабированные версии в пространстве сигнала. При этом сигнал s (t) может быть представлен множеством последовательных приближений sj (t) в субпространствах Vj.
Переменная j называется масштабным коэффициентом. Поскольку дерево декомпозиции сигнала при вейвлет-преобразовании принято отсчитывать вниз, значит сигнал s (t) есть предел аппроксимации sj (t))Î Vj
при j →-∞, т.е.
s (t)=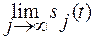 .
.
При больших j получаем грубые приближения сигнала, а при малых – точные. Приближение сигнала соответствует итерационной формуле:
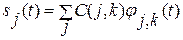 ,
,
причем
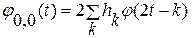 ,
,
где hk - некоторая последовательность. Сумма приближенной и детализирующей компонент дает исходный сигнал с тем или иным приближением.
Кратномасштабное представление лежит в основе многих применений вейвлет-анализа и вейвлет-преобразований. Например, применительно к сигналам изображений, оно означает представление изображений последовательностью образов с разной степенью их детализаций. При этом для создания грубого образа сигнала служит функция φ (t), а уточнение этого образа достигается с помощью вейвлет-функций или вейвлет-коэффициентов.
Первым типом вейвлета, на котором была теоретически доказана возможность кратномасштабного анализа (КМА) был вейвлет Хаара. На его примере было показано, что в ходе прямого и обратного дискретного вейвлет-преобразования возможно полное восстановление сигнала, если для целых k существуют такие коэффициенты { hk }, что
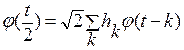 .
.
Это функциональное уравнение является одним из важнейших в теории вейвлет-анализа, и называется уравнением масштабирования или уравнением уточнения. Для функции Хаара можно найти, что коэффициенты 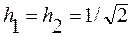 .
.
Добеши создала знаменитую серию вейвлетов, у которой, вейвлет db2 в сущности, является вейвлетом Хаара. Для получения вейвлета db4 Добеши использовала множество коэффициентов W ={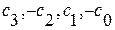 } и потребовала, чтобы линейная комбинация с векторами [1,1,1,1] и [1,2,3,4] была равна 0, т.е.
} и потребовала, чтобы линейная комбинация с векторами [1,1,1,1] и [1,2,3,4] была равна 0, т.е.
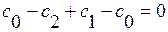 и
и 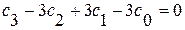 .
.
Используя эти соотношения в качестве условий нормирования и ортогональности, можно найти коэффициенты вейвлета Добеши db4:
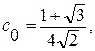
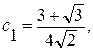
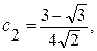
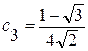 .
.
Уравнение масштабирования может иметь несколько иные формы записи, оно может быть задано в виде (x=t для временных зависимостей):
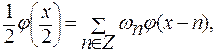 причем
причем 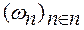 (9)
(9)
Вместо коэффициентов hk здесь использованы коэффициенты ωn и более удобная для большинства вейвлетов нормировка.
Дискретизация параметра a =2j означает возможность управления разрешением сигнала в ходе вейвлет-преобразований. Значения масштаба a и разрешения 1/ a представлены ниже в таблице 1.
Таблица 1 – Значения масштаба а и разрешения 1/ а.
| J | … | -1 | -2 | -3 | |||||
| Масштаб | … | 1/2 | 1/4 | 1/8 | |||||
| Разрешение | 1/210 | 1/29 | … | 1/4 | 1/2 |
 2014-02-13
2014-02-13 1898
1898
